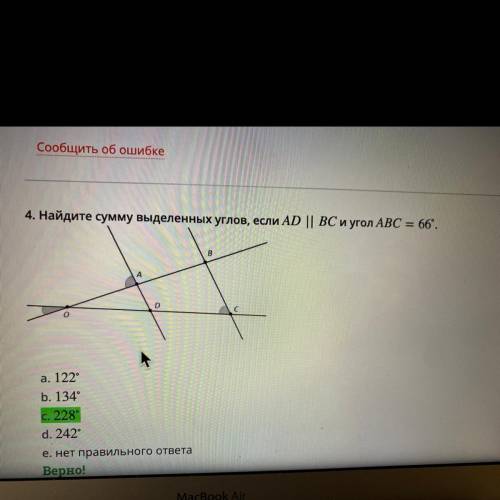
1) Пусть АВ – диаметр данной окружности, АС - хорда, АК - касательная.
В треугольнике АВС угол С=90° ( опирается на диаметр). АВ=2r, AC=r√3 ⇒ sin B=AC:AB ⇒ sin B=r√3:2r=√3/2.
Вписанный угол АВС равен половине дуги, на которую опирается. Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой (теорема) Следовательно, ∠КАС=∠АВС=arcsin √3/2 - это синус угла 60°.
* * *
2) Задача - обратная первой. Если угол КАС=60°, то вписанный угол АВС равен ему, т.е. ∠АВС=60°. Тогда хорда АС=АВ•sin60°=2r•√3/2=r√3
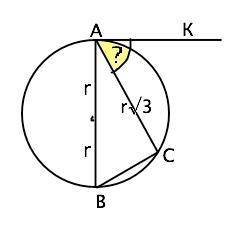
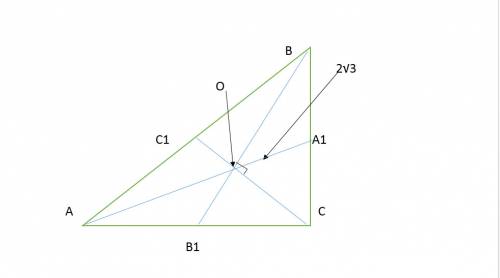
Объяснение:
<АВС=66
<ВАD=180-<ABC=180-66=114 как внутренние односторонние
<Aзакраш=<ВАD=114 как вертикальные
Сумма углов четырехугольника АВСD=360
<ABC+<BAD=180,значит <ВСD+ADC=180
Значит сумма противоположных углов равна 180,то <ВСD=180-<BAD=180-114=66
Тр-к ОBC:
<BOC=180-<OBC-<BCO
<OBC=<ABC=66
<BCO=<BCD=66
<BOC=180-66-66=48
<Oзакраш=<ВОС=48 как вертикальные
Сумма углов =<Озакр+<Азакр+<ВСD=
=48+114+66=228
ответ : С 228 градусов