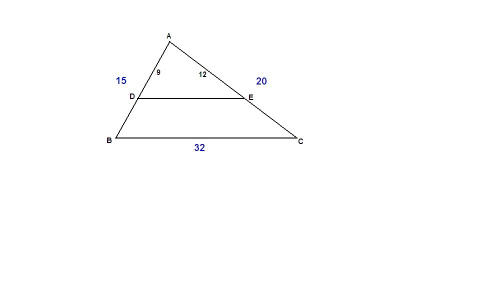
сделаем построение по условию
дополнительно
параллельный перенос прямой (BD) в прямую (B1D1)
искомый угол <AB1D1 в треугольнике ∆AB1D1
по теореме Пифагора
AB1=√(a^2+(3a)^2) =a√(1+9)= a√10
B1D1=√(a^2+(2a)^2) =a√(1+4)= a√5
AD1=√((2a)^2+(3a)^2) =a√(4+9)= a√13
по теореме косинусов
AD1^2 = AB1^2+B1D1^2 - 2*AB1*B1D1 * cos<AB1D1
(a√13)^2=(a√10)^2 + (a√5)^2 - 2* a√10* a√5 * cos<AB1D1
13a^2=10a^2 + 5a^2 -10√2a^2 * cos<AB1D1
cos<AB1D1 = 13a^2-(10a^2 + 5a^2) / -10√2a^2 = -2a^2 / -10√2a^2 = √2/10
<AB1D1 = arccos (√2/10)
ответ угол между прямыми BD AB1 arccos (√2/10)
ответ: Н = 6√3 см ; S біч = 576 см² .
Объяснение:
MABCD - 4-кутна піраміда ; ABCD - ромб ; АВ = 24 см ; ∠ А = ∠ С = 30° ;
MN⊥AB , MK⊥CD , ∠MNO = ∠MKO = . . .= 60° ;
проведемо BL║NK , BL⊥DC . Із прямок. ΔBLC BL = BCsin30° =
= 24*1/2 = 12 (см ) ; ON = OK = 1/2 * 12 = 6 (см ) .
Із прямок . ΔMON : MO = H = ON*tg60° = 6√3 cм ;
S біч = Р ос* MN ; P oc = 4* AB = 4 * 24 = 96 ( см ) ;
cos60° = ON/MN ; MN = ON : cos60° = 6 * 2 = 12 (см ) ;
S біч = 96 * 12 = 576 ( см² ) .