500 дм²
Объяснение:
Дано: пирамида, Sсечения=80 дм², сечение, параллельное основанию, делит высоту пирамиды в отношении 4:6, если считать от вершины.
Найти: S основания.
Решение: Так как получаются подобные многоугольники в сечении и в плоскости основания, то, зная площадь одного из них, можно найти с коэффициента подобия площадь основания.
Высота делится в отношении 4 к 6 от вершины. Значит всю высоту можно принять за 4+6=10 единиц, а расстояние до сечения от вершины за 4 единицы.
Значит коэффициентом подобия перехода от сечения к плоскости основания будет 10:4. Так как речь идет не о линейных измерениях, а о площадях, то надо умножать на коэффициент подобия в квадрате.
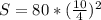
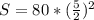
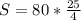
S=20*25
S=500 дм²
P.S. Если бы речь шла о подобных объёмных телах, то коэффициент подобия был бы уже в кубе.
30
Объяснение:
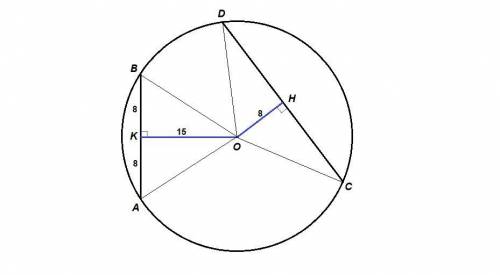
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и ОН⊥CD.
ОК = 15, ОН = 8 - расстояния от центра до хорд АВ и CD соответственно.
ΔАОВ равнобедренный, значит ОК - высота и медиана.
АК = КВ = 1/2АВ = 8
Из прямоугольного треугольника АОК по теореме Пифагора:
ОА = √(AK² + OK²) = √(8² + 15²) = √(64 + 225) = √289 = 17
ОС = ОА = 17
Из прямоугольного треугольника СОН по теореме Пифагора:
СН = √(CO² - OH²) = √(17² - 8²) = √(289 - 64) = √225 = 15
ΔOCD равнобедренный, значит ОН - высота и медиана.
CD = 2CH = 2 · 15 = 30
3) Р=40 ед
4) Р=22 ед
Объяснение:
3) если опустить ⊥ ВМ из вершины В на сторону АД получим прямоугольный ΔАВМ, ВМ- противолежащий катет, АВ - гипотенуза, ∠А=30
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе
тогда 5/АВ=sin30
5/AB=1/2
AB=10
Так как в ромбе все стороны равны АВ*4=40 - это и будет искомый периметр
4) мы знаем по условию что АВ+ВС+СД+АД=32 ед
Нам нужно найти АВ+ВЕ+АЕ
так как СД=ВЕ, ВС=5 и АД=АЕ+5, то можем записать
АВ+5+ВЕ+АЕ+5=32 ед
АВ+ВЕ+АЕ=22 ед
S осн =500 дм^2
Объяснение:
плоскость, параллельная основанию пирамиды, отсекает от пирамиды, пирамиду подобную ей.
секущая плоскость и основание пирамиды параллельны и подобны.
S сеч/Sосн=k^2
k - коэффициент подобия
высота делится в отношении 4:6, => высота 10
k=4:10, k=2/5
по условию известно, что площадь сечения =80 дм^2
(80/S осн)=(2/5)^2
Sосн =(80×25)/4
Sосн=500 дм^2