ответ: 262.44π.
Объяснение:
Площадь поверхности шара равна
V=4πR². (1)
Высота и радиус конуса и радиус вписанного шара связаны соотношением:
R/(H-R)=r/(√(H²-r²)), (2)
где Н=15,2 см - высота конуса.
r²=19²-15.2²= 361-231,04=129.96;
r=√129.96=11.4 см - радиус конуса.
Подставляем значения к и H в (2), получим:
R/(15.2-R)=11.4/(√(15.2²-11.4²));
R/(15.2-R)=11.4/10;
10R=11.4(15.2-R);
10R+11.4R=173.28;
21.4R=173.28;
R≈8.1 см - радиус шара.
Подставляем в (1), получим
S шара=4π8.1^2=262.44π.
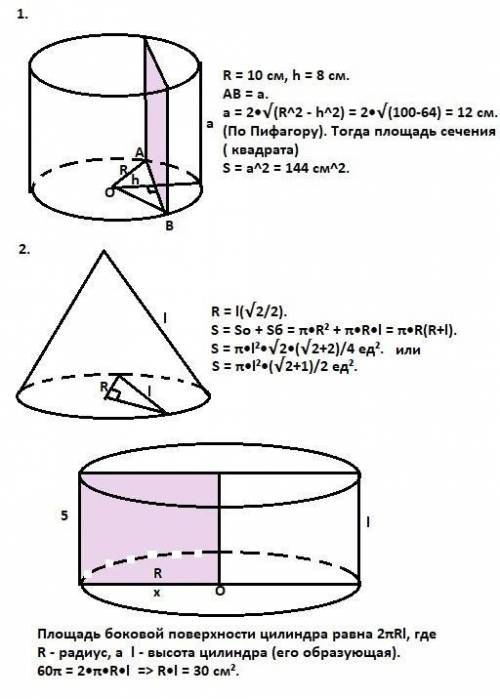
1. S = 144 см².
2. S = π•l²•(√2+1)/2 ед².
3. S = 30 см².
Объяснение:
Радиусы основания цилиндра, проведенные к концам хорды, являющейся стороной квадрата, образуют равнобедренный треугольник с основанием, равным этой стороне. Высота этого треугольника равна расстоянию от центра основания цилиндра до хорды. В равнобедренном треугольнике высота является и медианой. Следовательно, сторона квадрата равнa
а = 2•√(R^2 - h^2) = 2•√(100-64) = 12 см. (По Пифагору). Тогда площадь сечения ( квадрата) равна
S = a^2 = 144 см².
2. Площадь боковой поверхности конуса равна Sбок = π•R•l, а площадь основания конуса равна So = π•R², где R - радиус основания конуса, а l - его образующая. Хорда и проведенные к ее концам радиусы образуют равнобедренный прямоугольный (дано) треугольник с гипотенузой, равной этой хорде. Тогда по Пифагору гипотенуза этого треугольника равна l = R•√2, а катеты (радиусы основания) соответственно равны R = l•√2/2. Тогда площадь полной поверхности конуса равна
S = So + Sб = π•R² + π•R•l = π•R(R+l).
S = π•l²•√2•(√2+2)/4 ед² = π•l²•(√2+1)/2 ед².
3. Площадь боковой поверхности цилиндра, полученного вращением прямоугольника вокруг одной из его сторон, равна S = 2•π•R•l, где R - радиус основания цилиндра, а l - его высота. В нашем случае и радиус и высота - стороны прямоугольника, одна из которых равна 5 см. Тогда (независимо от того, чему равна одна из сторон прямоугольника) имеем:
60π = 2•π•R•l => R•l = 30 см². Это и есть площадь прямоугольника, вторая сторона которого в нашем случае равна 6 см.
ответ:129, 96
Объяснение: