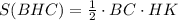, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.
.
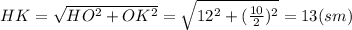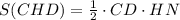, где НN - высота, проведенная к стороне СD.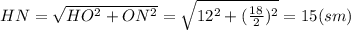
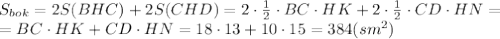
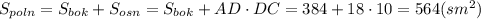
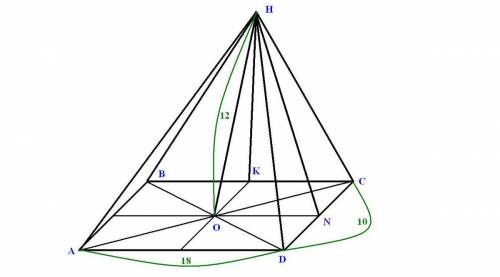
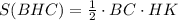, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.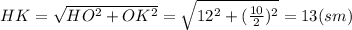.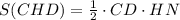, где НN - высота, проведенная к стороне СD.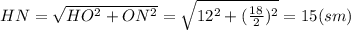
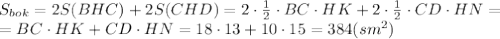
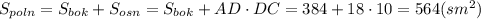
Объяснение:
a=3√3
Угол при вершине : α=180°-(30°+30°)=120°
S =1/2* a*a*sinα
S =1/2(3√3)²*sin120°
sin120°=sin60°=√3/2
S =1/2*9*3*√3/2
S =27√3/4