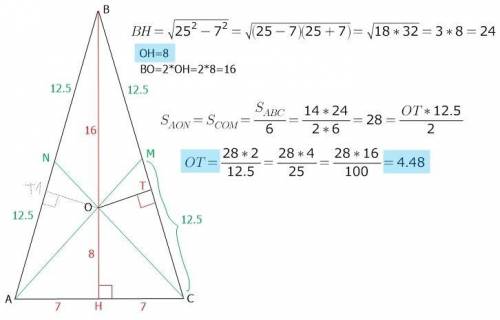
ответ: искомые расстояния 8 и 4.48
Объяснение:
→ Медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
→ Медиана делит треугольник на два равновеликих. Три медианы разделят треугольник на 6 равных по площади треугольников.
→ Расстояние от точки до прямой - отрезок перпендикуляра из точки к прямой.
две из трех медиан равнобедренного треугольника равны (проведенные к боковым сторонам)
Треугольник со сторонами 7,15,20 можно получить следующим образом. Берется "египетский" треугольник (то есть прямоугольный треугольник, подобный треугольнику со сторонами 3,4,5) со сторонами 12, 16, 20, на катете 16 от вершины прямого угла откладывается 9 и соединяется со вторым концом катета 12. При этом из треугольника 12,16,20 вырезается треугольник со сторонами 9, 12, 15 - тоже "египетский".
Таким образом, у треугольника 7,15,20 высота к стороне 7 равна 12. Площадь поверхности фигуры вращения равна сумме боковых площадей двух конусов, у которых радиус основания равен 12, высоты - 16 и 9, а образующие 20 и 15 соответственно.
2π*12*20 + 2π*12*15 = 2π*12*35 = 840π;
Примечание (касается всех!) Подобное решение, не смотря на то, что является строгим и верным, не будет принято и засчитано. Предложенное решение этой элементарной задачи очень полезно для понимания геометрии, и очень вам разобраться в сути вопроса, поскольку позволяет устно получить ответ, но "для учителя" необходимо (в соответствии с требованиями общеобразовательной системы) "обосновать" решение с стандартных методов.
В данном случае вы обязаны найти высоту треугольника к стороне 7, используя материал, данный вам на уроках. Наример, можно сосчитать площадь трегольника по формуле Герона, удвоить и разделить на 7. Это будет "строго". Но ,поскольку вы уже знаете ответ - это не составит труда.
В треугольнике со сторонами 25 см, 25 см, 14 см найдите расстояние от точки пересечения медиан до вершин треугольника.
ответ или решение 1
Стрелкова Полина
Для решения рассмотрим рисунок
Так как, по условию, АВ = ВС = 25 см, то треугольник АВС равнобедренный, а медиана ВН так же есть высота треугольника.
Медиана ВН делит основание АС пополам, тогда АН = СН = АС / 2 = 14 / 2 = 7 см.
В прямоугольном треугольнике АВН определим длину катета ВН.
ВН2 = АВ2 – АН2 = 625 – 49 = 576.
ВН = 24 см.
Медианы треугольника, в точке их пересечения, делятся в отношении 2 / 1, начиная с вершины.
Тогда ВО = 2 * ОН.
ВН = 24 = ОН + 2 * ОН = 3 * ОН.
ОН = 24 / 3 = 8 см.
ВО = 24 – 8 = 16 см.
В прямоугольном треугольнике АОН, АО2 = ОН2 + АН2 = 64 + 49 = 113.
АО = СО = √113 см.
ответ: Расстояние от точки пересечения медиан до вершин треугольника равно 8 см и √113 см.