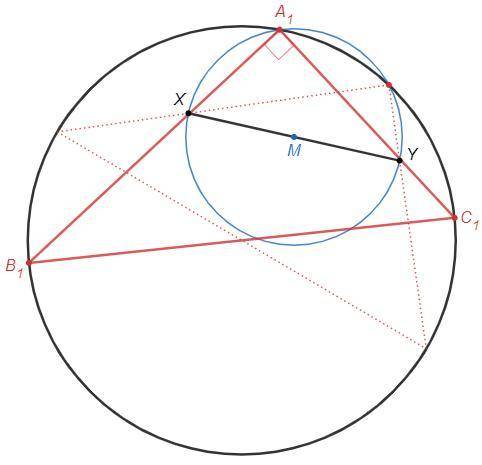
Дана окружность и точки X и Y внутри нее.
На отрезке XY как на диаметре построим окружность. Пересечения построенной окружности с данной окружностью - вершины треугольника (A1, A2).
Объяснение:
1) Построим середину отрезка XY - точку M.
(Для этого построим серединный перпендикуляр к отрезку:
- две дуги с центрами в концах отрезка
- прямую через точки пересечения дуг
Прямая пересечет отрезок в его середине)
Серединный перпендикуляр к отрезку - ГМТ, равноудаленных от двух точек.
2) Построим окружность с центром M радиусом MX.
Пересечение построенной окружности с данной окружностью - вершина А1 искомого треугольника.
Вписанный угол A1 - прямой, т.к. опирается на диаметр XY.
Окружность - ГМТ, из которых данный отрезок (диаметр) виден под прямым углом.
3) Проведем прямые A1X и A1Y. Их пересечения с данной окружностью - вершины B1 и С1 искомого треугольника.
Аналогично строим вершины B2 и С2, если имеется точка A2.
1. Запишем формулу площади трапеции:
2. Запишем формулу площади ромба:
S=ah; a=S/h=44/4=11
3. Запишем формулу периметра:
P=2(a+b)
16=2(a+b)
a+b=8
a=8-b
Запишем формулу площади и подставим вместо а, выражение 8-b.
S=ab=(8-b)*b=8b-b^2
12=8b-b^2
b^2-8b+12=0
D=64-4*12=16
b1=(8+4)/2=6
b2=(8-4)/2=2
Если ширина 6, то длина 8-6=2, если ширина 2, то длина 8-2=6
4. Наибольшей высотой будет та, которая опущена к меньшей стороне, т.е. к 17.
Найдем площадь по формуле Герона:
p=(17+65+80)/2=162/2=81
5. Найдём площадь по формуле Герон, но сначала найдем полупериметр:
P=(a+b+c)/2=(17+65+80)/2=81
[tex]S=\sqrt{81*(81-17)(81-65)(81-80)}=\sqrt{81*64*16*1}=288
Запишем формулу площади через высоту.
S=ah; h=S/a
найдём наибольшую высоту:
h1=288/17=16,9=17
h2=288/65=4,4
h3=288/80=3,6
Наибольшая высота равна 17.
6.Обозначим одну часть за х, тогда диагонали равны 2х и 3х. Запишем формулу площади через диагонали:
S=1/2 *d1*d2*sina ; sina=1 , т.к. диагонали ромба пересекаются под прямым углом.
2S=d1*d2
2*48=2x*3x
96=6x^2
x^2=16
x=4 (так как длина не может быть отрицательноц, то корень только один)