Рассмотрим все случаи неравенства треугольника. Всего 2 случая, НО только один из них верный. Докажем это.
Во-первых, вспомним, что сумма двух сторон треугольника должна быть больше третьей стороны.
Проверим это:
Возьмём случай, где основание нашего равнобедренного треугольника равно 72 см, а боковые стороны по 36 см, ибо они по правилу равны. Проверим, существует ли такой треугольник, следуя теореме (выделена выше наклонным курсивом).
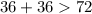 - это неверно;
- это неверно;
 - это верно;
- это верно;
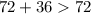 - это верно.
- это верно.
Поскольку первый случай неверный, то такого треугольника не существует.
То есть боковые стороны нашего треугольника равны по 72 см.
(рисунок к задаче прикреплён ниже)
ответ: 5).→ Задача №6.Гипотенуза - самая большая сторона в прямоугольном треугольнике, поэтому она не может равняться в данной задаче 11 см, поскольку это не самая большая цифра здесь. Получается подходит вариант 5) 11 см, т.к. гипотенуза всегда больше катета.
ответ: 5).
В каждой вершине параллелепипеда сходятся смежные стороны трех граней, и их диагонали образуют треугольник. (см. рисунок вложения)
В данном случае диагонали равны 30, 40 и 70 см.
По теореме о неравенстве треугольников: длина любой стороны треугольника меньше суммы длин двух других сторон.
Здесь имеем "треугольник" и три длины, и 70=30+40.
Тогда меньшие стороны "лягут" на большую, и треугольник не получится, как и параллелепипед с такими диагоналями граней.
Не могут диагонали трех граней прямоугольного параллелепипеда иметь длины 30 см, 40 см и 70 см.