Площадь трапеции равна произведению её высоты на полусумму оснований ( среднюю линию).
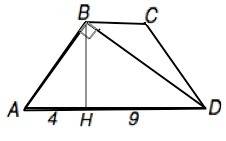
Обозначим трапецию АВСD, высоту - ВН. Тогда АН=4, DH=9
Высота равнобедренной трапеции делит основание на отрезки, меньший из которых равен полуразности оснований, больший – их полусумме. ⇒
S=BH•HD
Треугольник АВD- прямоугольный.
Его высота – общая с высотой трапеции.
Высота прямоугольного треугольника, проведенная из прямого угла - среднее пропорциональное между отрезками, на которые она делит гипотенузу.
ВН²=АН•DH=4•9=36
BH=√36=6
S(трап)=6•9=54.
Сделаем рисунок. Соединим точки А и Е.
Рассмотрим треугольники АСД и АСЕ.
∠ АСД=∠ АСЕ, это угол - общий для обоих треугольников
∠САД равен ∠ СЕА, так как они опираются на равные дуги
( Треугольник АСВ равнобедренный по условию, и ∠САВ =∠СВА, который опирается на ту же дугу, что и СЕА.
Итак, имеем два треугольника с двумя равными углами .
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Следовательно, Δ АСД ~ Δ АСЕ.
Из подобия треугольников:
AC:DC = СЕ:AC
АС:1,5=3:АС
АС²=4,5
АС=√2,25·2=1,5√2