Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство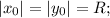
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) 
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
;
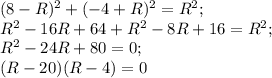R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
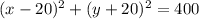
и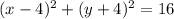 
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили
ответ: БИЛЕТ№1
1. отрезок -прямая, которая имеет начало и конец, обозначается с обоих сторон точками.
луч - это прямая линия, которая имеет начало, но не имеет конца.
угол - это геометрическая фигура, образованная 2-мя лучами
развернутый угол-это угол, стороны которого составляют прямую
2. если две стороны и угол между ними одного треугольника соответственно равны двум сторонам между ними другого треугольника, то такие треугольники равны
3. т.к. треугольник прямоугольный, а один из углов 30гр, то второй катет будет равен половине гипотенузы 12*2=24см
4.т.к треуг.АВС равноб. следовательно углы при основании равны, а т.к. угол 1 вертикальный углу ВАС, значит они равны
2 вертик угол ВС, а следовательно они равны
угол1 = углу ВАС, угол 2 - углу ВСА
следовательно углы =
Відповідь:
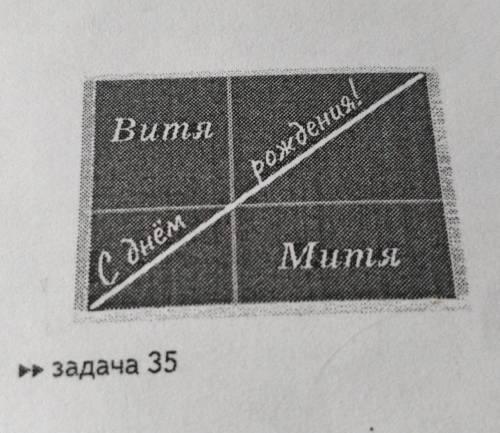
Площадь куска с надписью "Витя" равна площади куска с надписью "Митя".
Пояснення:
Пусть длина торта равна Х = Х1 + Х2, где Х1 - длина левой части ( там где написано "Витя" ), а Х2 - длина правой части ( там где написано "Митя" ).
Пусть ширина торта равна У = У1 + У2, где У1 - ширина верхней части ( там где написано "Витя" ), а У2 - ширина нижней части ( там где написано "Митя" ).
Тогда площадь куска с надписью "Витя" равна S1 = Х1 × У1, а площадь куска с надписью "Митя" равна S2 = Х2 × У2.
Поскольку в прямоугольнике проведена диагональ, то должна выполняться пропорция:
Х / У = Х1 / У2 = Х2 / У1 ( в пропорции индексы 1 и 2 возле Х и У не совпадают, так как мы привязали номера к кускам с именами и взяли номера Х слева на право, а номера У сверху вниз ).
Приведем уравнение для площади куска с надписью "Митя" ( S2 = Х2 × У2 ) к индексам Х1 и У1.
Из пропорции:
Х2 / У1 = Х1 / У2
Получаем:
Х2 = Х1 × У1 / У2
Подставим в уравнение для S2:
S2 = Х2 × У2 = Х1 × У1 × У2 / У2 = Х1 × У1 = S1
В результате мы получили, что площадь куска с надписью "Витя" равна площади куска с надписью "Митя".