
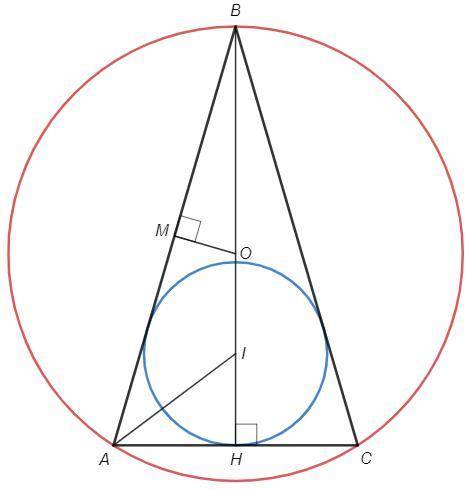
Равнобедренный треугольник, основание AC=14.
BH - высота к основанию, является также биссектрисой и медианой.
AH=AC/2 =7 (H - середина AC)
BH =√(AC^2 -AH^2) =24 (теорема Пифагора)
S(ABC) =AC*BH/2 =14*24/2 =168
Центр вписанной окружности (I) - точка пересечения биссектрис.
BI/IH =AB/AH =25/7 (теорема о биссектрисе)
IH =7/32 BH =21/4 =5,25
(IH - расстояние от центра до стороны, то есть радиус)
Центр описанной окружности (O) - точка пересечения серединных перпендикуляров.
M - середина AB, BM=25/2
△OBM~△ABH (по двум углам)
OB/AB =BM/BH
OB =25*25/2*24 =625/48 ~13,02
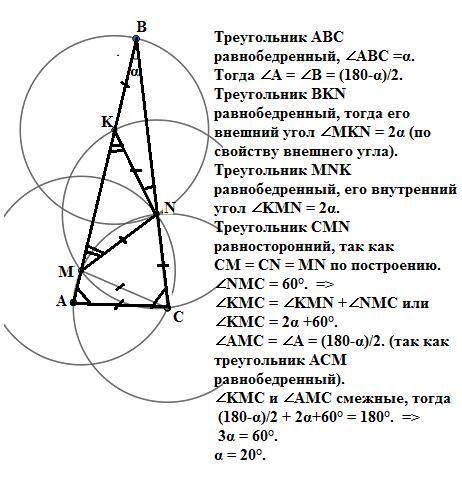
∠АВС = 20°.
Объяснение:
Треугольник АВС равнобедренный, ∠ABC =α.
Тогда ∠A = ∠В = (180-α)/2.
Треугольник BKN равнобедренный, тогда его внешний угол
∠MKN = 2α (по свойству внешнего угла).
Треугольник MNK равнобедренный, его внутренний угол
∠KMN = 2α.
Треугольник CMN равносторонний, так как
CM = CN = MN по построению.
∠NMС = 60°. =>
∠KMC = ∠KMN +∠NMС или
∠KMC = 2α +60°.
∠АMС = ∠A = (180-α)/2. (так как треугольник АСМ равнобедренный).
∠KMС и ∠АMС смежные, тогда
(180-α)/2 + 2α+60° = 180°. =>
3α = 60°.
α = 20°.
60°; 120°
Р(АВСD)=16 ед
Объяснение:
Рассмотрим треугольник ∆ВDP
BD=4 ед гипотенуза
PD=2 ед катет
Катет в два раза меньше гипотенузы, когда катет против угла 30°
<РВD=30°
Сумма острых углов в прямоугольном треугольнике равна 90°
<РDB=90°-<PBD=90°-30°=60°
Диагональ ромба является биссектриссой его углов.
ВD- биссектрисса угла <АDC
<ADC=2*<PDB=2*60°=120°
Сумма углов прилежащих к одной стороне ромба равна 180°
<ВАD=180°-<ADC=180°-120°=60°
В ромбе с углами 60°; 120°, меньшая диагональ равна стороне ромба.
ВD=AB=4ед
P(ABCD)=4*AB=4*4=16 ед.