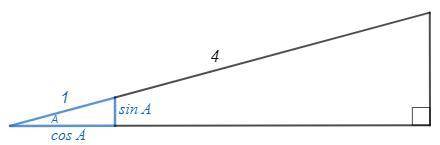
Рассмотрим треугольник, подобный данному с коэффициентом 1/4.
Его гипотенуза 1, площадь 1/8, катеты sinA и cosA.
S =1/2 sinA cosA =1/8 => 2 sinA cosA =1/2 =sin(2A) => 2A=30 => A=15°
B=90-15 =75°
Дана окружность и точки X и Y внутри нее.
На отрезке XY как на диаметре построим окружность. Пересечения построенной окружности с данной окружностью - вершины треугольника (A1, A2).
Объяснение:
1) Построим середину отрезка XY - точку M.
(Для этого построим серединный перпендикуляр к отрезку:
- две дуги с центрами в концах отрезка
- прямую через точки пересечения дуг
Прямая пересечет отрезок в его середине)
Серединный перпендикуляр к отрезку - ГМТ, равноудаленных от двух точек.
2) Построим окружность с центром M радиусом MX.
Пересечение построенной окружности с данной окружностью - вершина А1 искомого треугольника.
Вписанный угол A1 - прямой, т.к. опирается на диаметр XY.
Окружность - ГМТ, из которых данный отрезок (диаметр) виден под прямым углом.
3) Проведем прямые A1X и A1Y. Их пересечения с данной окружностью - вершины B1 и С1 искомого треугольника.
Аналогично строим вершины B2 и С2, если имеется точка A2.
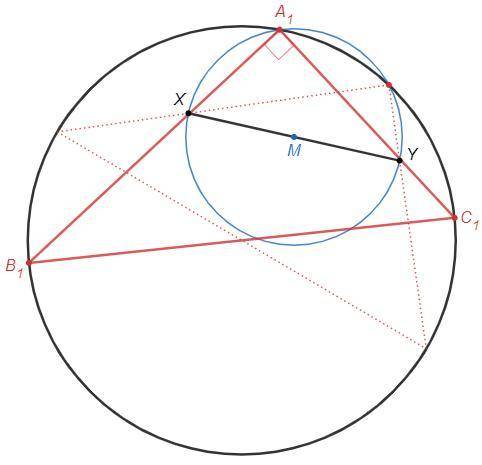
Дана окружность и точки X и Y внутри нее.
На отрезке XY как на диаметре построим окружность. Пересечения построенной окружности с данной окружностью - вершины треугольника (A1, A2).
Объяснение:
1) Построим середину отрезка XY - точку M.
(Для этого построим серединный перпендикуляр к отрезку:
- две дуги с центрами в концах отрезка
- прямую через точки пересечения дуг
Прямая пересечет отрезок в его середине)
Серединный перпендикуляр к отрезку - ГМТ, равноудаленных от двух точек.
2) Построим окружность с центром M радиусом MX.
Пересечение построенной окружности с данной окружностью - вершина А1 искомого треугольника.
Вписанный угол A1 - прямой, т.к. опирается на диаметр XY.
Окружность - ГМТ, из которых данный отрезок (диаметр) виден под прямым углом.
3) Проведем прямые A1X и A1Y. Их пересечения с данной окружностью - вершины B1 и С1 искомого треугольника.
Аналогично строим вершины B2 и С2, если имеется точка A2.

или
15° и 75°
Объяснение:
Обозначим в прямоугольном треугольнике
катеты как a, b
гипотенузу как с (с = 4)
и углы как
Причем углы связаны формулой
Тогда площадь треугольника, равная 2, равна половине произведения катетов:
Однако для острого угла в прямоугольном треугольнике отношение прилежащего катета к гипотенузе - это косинус угла, а отношение противолежащего катета к гипотенузе - это синус угла
Соответственно, каждый из катетов можно выразить через синус и косинус одного из острых углов:
Т.к. с = 4, получаем:
Получаем ригонометрическое уравнение:
Т.к. мы ищем углы в прямоугольном треугольнике, то
Соответственно попадают в этот интервал только следующие полученные углы:
Итак, мы получили 2 пары углов:
Очевидно, что это одна и та же пара углов, в зависимости от того, какой катет мы брали за а, а какой за b.
Итак, получаем ответ: