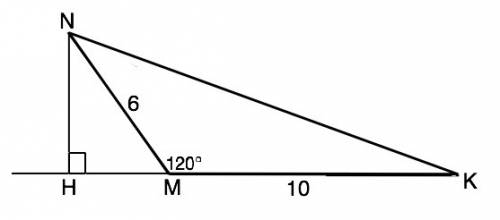
Проведем высоту из вершины N. Для тупоугольного треугольника высота из вершины острого угла пройдет вне его и пересечет продолжение стороны, в данном случае стороны МК в точке Н. В треугольнике NHM угол NMH=180°-120°=60° ( как смежный углу NMK). Тогда НМ=MN•cos60°=3 см, а катет NH=NM•sin60°=3√3 см. НК=НМ+МК=3+10=13 см. По т.Пифагора NK=√(NH²+HM²)=√196=14 см. Найдем угол К=NH:НК=3√3:14=arcsin 0,3712, что соответствует углу 21,786° или 21°47’. Из суммы углов треугольника угол N=180°=(120°+21°47´)=38°13´
———————
Эту задачу можно также решить с применением т.косинусов и затем т.синусов.
S=6√3см²
с=√46см
Объяснение:
Дано:
Треугольник
а=4см сторона треугольника
b=6см сторона треугольника
<(ab)=60° угол между сторонами а и b
S=? площадь треугольника
c=? сторона треугольника
Решение
S=1/2*a*b*sin(<ab)
sin60°=√3/2
S=1/2*6*4*√3/2=6√3 см²
Теорема косинусов
с=√(а²+b²-2ab*cos(<ab))
cos60°=1/2
c=√(6²+4²-2*6*4*1/2)=√(36+16-6)=
=√46 см