а - сторона ромба
периметр
Р = 4 а = 52
а = 52/4 = 13 см
Диагонали ромбы d1 и d2 перпендикулярны = >
d1 / d2 = 5 / 12 или d1 = 5d2 / 12
Cтороны прямоугольных треугольников, образуемых диагоналями, будут ^
d1/2, d2/2 - катеты
а - - гипотенуза (она же сторона ромба)
По теореме пифагора
(d1/2) ^2 + (d2/2) ^2 = a^2
d1^2 + d2^2 = 4a^2
(5d2 / 12) ^2 + d2^2 = 13^2
25d2^2 + 144d2^2 = 13^2 * 12^2
169d2^2 = (13^2*12^2
13^2 d2^2 = 13^2 * 12^2
d2^2 = 12^2
d2 = 12 см - вторая диагональ
d1 = 5d2 / 12 = 5 * 12 / 12 = 5 - первая диагональ
ответ: диагонали d1=5 cм, d2 = 12 см
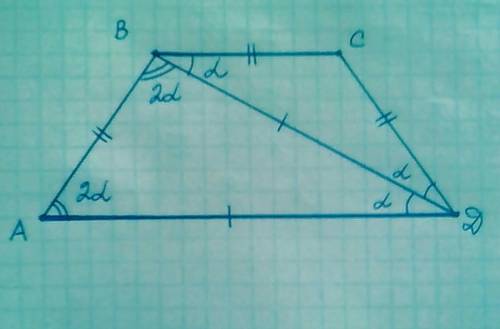
1) Рассмотрим ∆ ВСD:
Пусть угол CBD = a , тогда угол BDC = a, так как ∆ ВСD - равнобедренный
угол СBD = угол АDB = a - как накрест лежащие углы при ВС || АD и секущей BD
По свойству равнобедренной трапеции:
Углы при основании равнобедренной трапеции равны
Значит, угол BAD = угол ADC = 2a
2) Рассмотрим ∆ ABD:
∆ ABD - равнобедренный , поэтому угол BAD = угол АВD = 2a
Сумма всех углов в любом треугольнике всегда равна 180° =>
угол ВАD + угол ABD + угол ADB = 180°
2a + 2a + a = 180°
5a = 180°
a = 180° : 5 = 36°
Угол при меньшем основании ( ВС ) равнобедренной трапеции равен:
угол ABC = 3a = 3 × 36 = 108°
ОТВЕТ: 108°
4; 1), (-3;1), (-2;0), (-4;-1), (-3;-2), (-2;-2), (-1;-1), (-1;-2), (0;-3), (1;-3), (3;-2), (4;0), (4;2), (6;3), (4;3), (5;4), (3;4), (4;5), (4;7), (2;8), (3;6), (2;5), (2;6), (1;8), (1;6), (0;7), (-1;7), (0;6), (0;5), (-1;6), (-2;6), (-3;5), (-2;5), (0;4), (-2;4), (-4;3), (-4;1), (-5;4), (-6;5), (-5,5;3,5), (-7;4), (-7,5;3),
(-6;3), (-8;1), (-7;1), (-6;-2), (-4;-3), (-4; -7), (-3;-8), (-4;-9), (-3;-9),
(-4;-11), (-3;-11), (-2;-9), (-1;-9), (-1;-8), (0,-8), (0;-9), (1;-9), (2;-11), (3;-11), (2;-9), (3; -9), (2;-8), (2;-7), (4;-8), (4;-7), (6;-7), (5; -6), (7;-6), (5;-5), (6;-5), (4;-4), (3;-2).
ГЛАЗ (0;1), (1;1), (1;0), (0,5;0,5).