ответ: площадь треугольника равна 12см^2.
Объяснение:
Площадь треугольника можно вычислить по формуле:
S=(1/2)*a*b*sina, где а и b - стороны треугольника, а sina - синус угла между этими сторонами.
S=(1/2)*6*8"(1/2)=12см^2.
Или так: проведем высоту ВН к стороне АС. Это катет, лежащий против угла 30°. Он равен половине гипотенузы.
Тогда если сторона АВ=6см (гипотенуза), а сторона АС=8см, то ВН=3см и площадь треугольника равна S=(1/2)*AC*BH =(1/2)*8*3=12см^2.
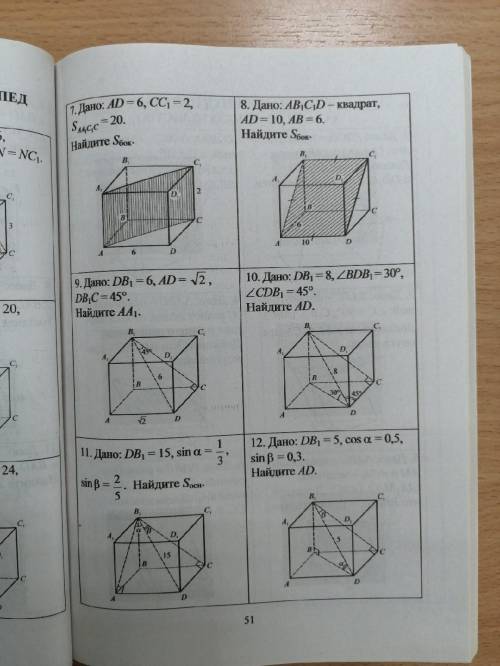
Если АВ=8см, а АС=6см, то ВН=4см и S=(1/2)*6*4=12см^2.
Внешний угол правильного многоугольника и его внутренний угол являются смежными, значит, их сумма равна 180°.
Т.к. по условию задачи внутренний угол в 8 раз больше внешнего, то пусть внешний угол х°, тогда внутренний угол будет равен (8х)° (см. рис.). Составим и решим уравнение:
х + 8х = 180.
9х = 180,
х = 180 : 9,
х = 20.
Значит, внутренний угол правильного многоугольника равен
8 · 20° = 160°.
Внутренний угол правильного многоугольника находят по формуле:
180° · (n - 2) / n, где n - число сторон правильного многоугольника.
Имеем:
180° · (n - 2) / n = 160°,
180° · (n - 2) =160° · n,
9 · (n - 2) = 8 · n,
9n - 18 = 8n,
9n - 8n = 18,
n = 18.
Значит, наш правильный многоугольник имеет 18 сторон.
ответ: 18 сторон.
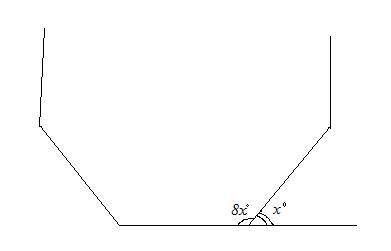
Объяснение:
8)
АВ1=АD=10ед. АВ1С1D- квадрат.
∆АВ1В- прямоугольный треугольник
По теореме Пифагора
ВВ1=√(АВ1²-АВ²)=√(10²-6²)=8 ед.
Sбок=Р(АВСD)*ВВ1=2(6+10)*8=256 ед²
ответ: 256ед²
9)
∆DB1C- прямоугольный равнобедренный треугольник. (<DB1C=45°; <B1CD=90°; <B1DC=45°) углы при основании равны.
В1С=В1D/√2=6/√2=3√2 ед
ВС=AD=√2 ед
∆ВВ1С- прямоугольный треугольник
По теореме Пифагора
ВВ1=√(В1С²-ВС²)=√((3√2)²-(√2)²)=√(18-4)=
=√15 ед.
ответ: АА1=√15 ед.
10)
В1В=В1D/2=8/2=4 ед катет против угла 30°
∆ВВ1D- прямоугольный треугольник
По теореме Пифагора
ВD=√(B1D²-B1B²)=√(8²-4²)=4√3 ед.
∆DB1C- прямоугольный, равнобедренный треугольник.
DC=B1C
DC=B1D/√2=8/√2=4√2 ед.
∆ВСD- прямоугольный треугольник
По теореме Пифагора
ВС=√(ВD²-DC²)=√((4√3)²-(4√2)²)=
=√(16*3-16*2)=√(48-32)=√16=4 ед.
ВС=АD=4ед
ответ: AD=4 ед.