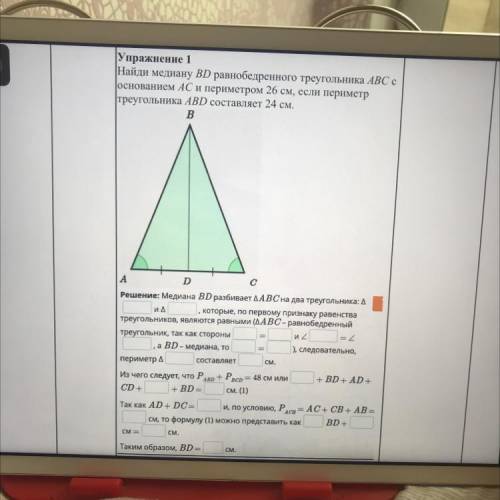
66° и 42°
Объяснение:
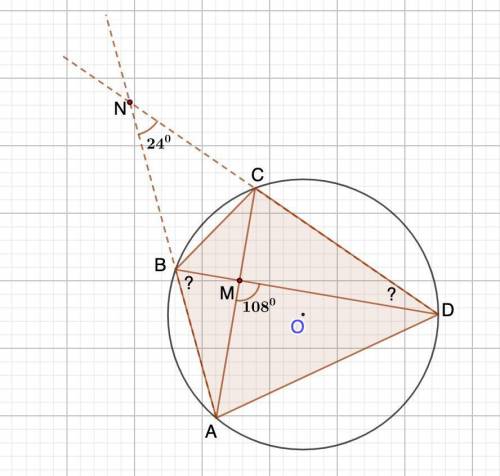
Дано: Окр.О;
АВСD - вписанный четырехугольник;
АС ∩ BD = M; AB ∩ BC = N;
∠АMD = 108°; ∠AND = 24°.
Найти: ∠АBD и ∠BDC.
1.
Угол между пересекающимися хордами окружности равен полусумме двух противоположных дуг, высекаемых этими хордами.⇒
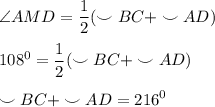 (1)
(1)
⇒
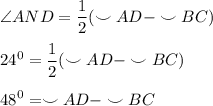 (2)
(2)
Из (2) выразим дугу AD и подставим в (1):
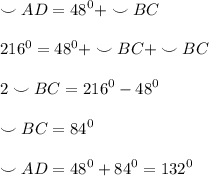
2. Теперь можем найти искомые углы.
Вписанный угол равен половине градусной меры дуги, на которую он опирается.⇒
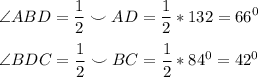
Объяснение:
площадь трапеции
площадь трапеции равна произведению полусуммы ее оснований на высоту:
s = ((ad + bc) / 2) · bh,
где высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
доказательство.

рассмотрим трапецию abcd с основаниями ad и bc, высотой bh и площадью s.
докажем, что s = ((ad + bc) / 2) · bh.
диагональ bd разделяет трапецию на два треугольника abd и bcd, поэтому s = sabd + sbcd. примем отрезки ad и bh за основание и высоту треугольника abd, а отрезки bcи dh1 за основание и высоту треугольника bcd. тогда
sabc = ad · bh / 2, sbcd = bc · dh1.
так как dh1 = bh, то sbcd = bc · bh / 2.
таким образом,
s = ad · bh / 2 + bc · bh = ((ad + bc) / 2) · bh.это можно только с доказательством