1.
Пусть одна из сторон параллелограмма х см, тогда другая х+5 см.
Сумма двух смежных сторон (полупериметр) параллелограмма р=66:2=33 см. Составим уравнение:
х+х+5=33; 2х=28; х=14.
Одна сторона 14 см, смежная сторона 14+5=19 см.
ответ: 14 см, 14 см, 19 см, 19 см.
2.
Диагонали прямоугольника равны и в точке пересечения делятся пополам.
АО=ВО=1/2 АС = 20:2= 10 см
Р(АОВ)=АВ+ОВ+АО=15+10+10=35 см.
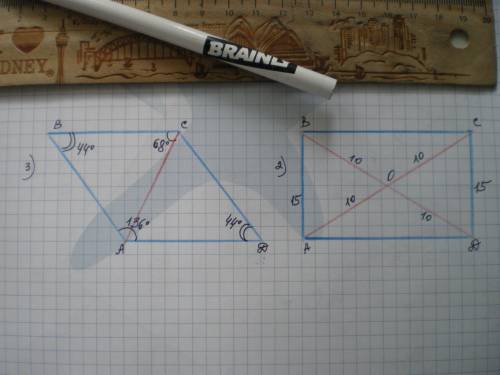
3.
Противоположные углы ромба равны. Диагонали ромба перпендикулярны и делят углы ромба пополам.
Рассмотрим ΔАВС - равнобедренный, т.к. АВ=ВС как стороны ромба.
∠ВСА=∠ВАС=68°.
∠В = ∠D = 180-68*2=44°
∠А=∠С=68*2=136°
Відповідь:
ВС = 8 см.
Пояснення:
1) Трикутник АВС - прямокутний ( кут С = 90° ), АВ - гіпотенуза.
За теоремою Піфагора:
ВС^2 = АВ^2 - АС^2 = 100 - 36 = 64
ВС = 8 см.
2) Прямокутний трикутник АВС - є подібним до єгипецького трикутника з відношенням сторін 5 : 4 : 3. Коєфіцієен подобія дорівнює 2. Якщо ми помножимо на 2 сторони єгипецького трикутника, то отримаємо відношення сторін: 10 : 8 : 6. Відповідно якщо АВ = 10 см., АС = 6 см., то ВС = 8 см.