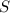данного сечения = 
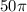ед.кв.
Объяснение:
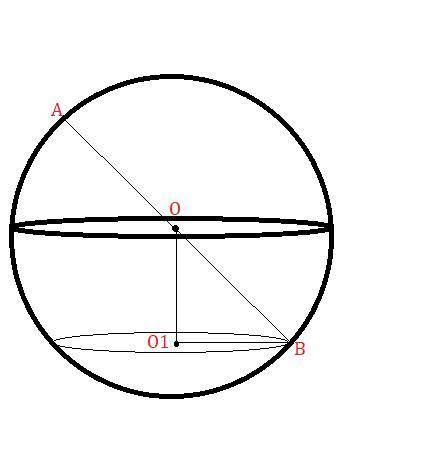
Пусть будет дан шар с центром в точке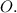 
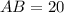ед.
Через точку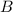 
проведём плоскость под углов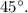 
Пусть будет плоскость с центром в точке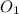 
.
Тогда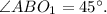 
========================================================
Так как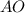 
и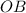 
- радиусы данного шара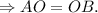 
Т.е.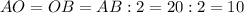 
ед.
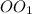
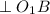, так как 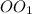- серединный перпендикуляр.
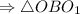- прямоугольный.
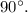
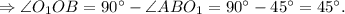
Так как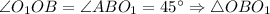 
- равнобедренный.
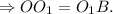
Пусть 
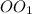- и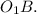 
По теореме Пифагора:
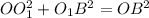
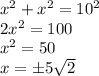
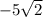- отрицательное число, поэтому не подходит.
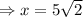
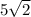ед. -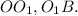 
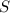данного сечения = 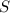круга = 
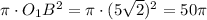ед.кв.
Признак параллельности прямой и плоскости
Если прямая, не лежащая в плоскости, параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна и самой плоскости
•Доказательство Метод «от обратного» Пусть а не параллельна α. Тогда… а содержится в α. или а пересекает α. По лемме, так как а ║ b, то b тоже пересекает α. Это противоречит условию теоремы. Значит, наше предположение неверно. Следовательно а ║ α
•Если одна из двух параллельных прямых параллельна плоскости, то другая прямая… •либо также параллельна данной плоскости, •либо лежит в этой плоскости.