Дана окружность с центром в точке О и радиусом r и прямая р.
d - расстояние от центра окружности до прямой р.
Могут ли d и r быть равными?
а) нет, d всегда больше r
;
б) да; в этом случае прямая p называется секущей по отношению к окружности
;
в) нет, d всегда меньше r
;
г) да; в этом случае прямая p называется касательной по отношению к окружности.
110 мм
г)
Объяснение:
1 дм = 100 мм, значит
1,1 дм = 110 мм
________________________________
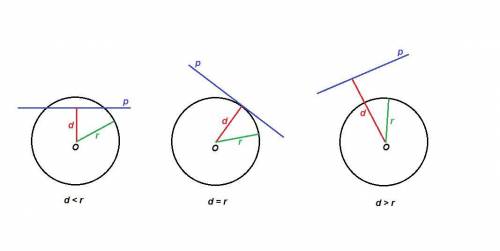
Есть три возможных случая взаимного расположения прямой и окружности:
прямая пересекает окружность в двух точках (прямая является секущей к окружности), тогда d < r;прямая и окружность имеют одну общую точку (прямая является касательной к окружности), тогда d = r;прямая и окружность не имеют общих точек, тогда d > r.Могут ли d и r быть равными?
Да. В этом случае прямая p называется касательной по отношению к окружности.
сделаем построение по условию
перпендикуляр к плоскости - это отрезок DC=a
<C=90 ; катет АС =а ; <B = <(альфа)
гипотенуза AB
DK ┴ AB
CK ┴ AB
DC ┴ CK
по теореме о трех перпендикулярах СK - это проекция DC
DK=b, CK=d -расстояние от концов отрезка DC до гипотенузы
так как прямые (СК)┴(АВ) ;(BС)┴(АC) взаимно перпендикулярные,то <KCA=<B=<альфа
∆KAC - прямоугольный
d = a*cos<альфа
∆KDC - прямоугольный
по теореме Пифагора
b = √ (d^2+a^2) =√((a*cos<альфа)^2+a^2) = a*√((cos<альфа)^2+1)
ответ
d = a*cos<альфа
b = a*√((cos<альфа)^2+1)