Точка К проецируется на плоскость треугольника в точку О - центр описанной окружности, т.к. прям. тр-ки АКО, ВКО и СКО - равны (АК=ВК=СК=8, КО - общий катет). АО = ВО = СО = R - радиус описанной окр-ти.
Найдем R, используя две формулы для площади тр-ка:
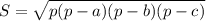 (1)
(1)
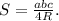 (2)
(2)
p=(5+5+8)/2 = 9
Из (1) получим:
S =кор(9*4*4*1) = 12
Тогда из (2):
R = (5*5*8)/(4*12) = 25/6
Теперь из пр. тр-ка АКО найдем искомое расстояние КО по т. Пифагора:
КО = кор(AK^2 - AO^2) = кор(64 - 625/36) = (кор1679)/6 = 6,8 (примерно)
ответ: 6,8 см (примерно)
4 остальные стороны - следы сечения боковых граней призмы.
Они равны √(5²+(11/2)²) = √(25+30,25) = √55,25.
Высота шестиугольника равна √(АС²+СС1²) = √((2acos30°)²+11²) =
= √((2*5*(√3/2))² + 121) = √(75+121) = √196 = 14.
Площадь шестиугольника S равна сумме площадей прямоугольника S1 и двух треугольников, площадь S2 которых можно найти по формуле Герона.
S1 = 5*14 = 70.
S2 = 2√(p(p-a)(p-b)(p-c), где р - полупериметр, равный (а+в+с)/2 =
= (14+2*√55,25)/2 = 7+√55,25 ≈ 14,43303.
Тогда S2 = 2*17,5 = 35.
ответ: S = 70 + 35 = 105.