проводим касательную, проводим радиусы в точки касания, и соединяем центры. кроме того, из центра меньшей окружности проводим пепендикуляр к радиусу большей окружности, проведенном у точку касания. этот перпендикуляр равен общей касательной (там прямоугольник: получился прямоугольный треугольник со сторонами d = корень(80) - линия центров, это гипотенуза треугольника, (r - r), и второй катет в качестве искомого расстояния.
x^2 = d^2 - (r - r)^2;
по условию r - r = 4; x^2 = 80 - 16 = 64; x = 8;
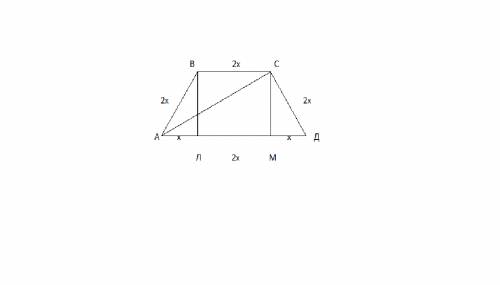
Из треугольника АСД: уголД=60гр., Угол АСД=90гр., отсюда угол САД=30гр.
Так, как АС это биссектриса угла ВАД, то угол ВАД=САД+ВАС=30гр.+30гр.=60гр.
Отсюда можно сделать вывод, что трапецыя АВСД- равнобедренная.
Из треугольника АВС:
Угол ВСА=ВСД-АСД=120гр.-90гр.=30гр.; уголВАС=углуВСА, отсюда треугольникАВС-равнобедренный.
Отсюда АВ=ВС=СД.
Проведем высоты ВЛ и СМ.
Треугольник АВЛ = треугольнику СМД, за тремя сторонами равными.
Так, как МД лежит против угла 30гр., в прямоугольном треугольнике, то 2МД=ДС.
Пускай МД=АЛ=х, ЛМ=ВС=АВ=СД=2х. Так, как сума всех этих сторон равна 35 см., то имеем уравнение:
2х+2х+2х+2х+х+х=35
10х=35
Х=35/10
Х=3,5
Значит АВ=2х=2*3,5=7см.
ответ:7см.
Объяснение:
6) Обозначим вершины треугольника АВС. R радиус описанной окружности найдём по формуле:
R=(abс)/(4S) где abc – стороны треугольников, а S –его площадь.
где р – полупериметр.
р=(АВ+ВС+АС)/2=(13+14+15)/2=42/2=21
S=84(ед²)
R=(13×14×15)/(4×84)=2730/336=8,125(ед)
r=S/p – где r –радиус вписанной окружности, а р – полупериметр.
r=84/21=4(ед)
ОТВЕТ: r=4(ед); R=8,125(ед)
7) а(2; –6); b(–6; 2); c(2a+b)–?
2a=(2×2; –6×2)=(4; –12)
2a+b=(4+(–6); –12+2)=(–2; –10)
2a+b(–2; –10)
Абсолютная величина вектора 2а+b:
ОТВЕТ: координаты вектора 2а+b(–2; –10);
абсолютная величина вектора 2а+b=2√26