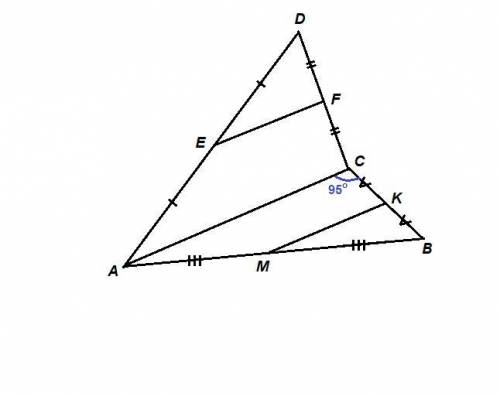
Треугольники АВС и ADC не лежат в одной плоскости. Точки Е, F, M, K - середины соответственно отрезков AD, CD, AB и ВС. ∠АСВ = 95°.
Найти угол между прямыми:
1) EF и МК
2) EF и ВС
1) 0°
2) 95°
Объяснение:
1)
EF║AC как средняя линия треугольника ADC,
MK║AC как средняя линия треугольника AВC, значит
EF║MK по свойству параллельности прямых.
Угол между параллельными прямыми равен 0°.
2)
Прямая EF лежит в плоскости (ADC), прямая ВС пересекает плоскость (ADC) в точке С, не лежащей на прямой EF, значит прямые EF и ВС скрещивающиеся по признаку.
Угол между скрещивающимися прямыми - это угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.EF║AC, тогда
∠(EF, BC) = ∠(AC, BC) = ∠ACB = 95°
_______________________________________
В условии задачи дан ∠АВС = 95°, но, вероятно, это опечатка, так как при таком условии ответить на второй вопрос нельзя.
∠B = 53°; S=900мм²
Объяснение:
Поперечный разрез паза имеет форму равнобедренной трапеции.
Нам надо найти угол В и площадь данной трапеции.
1. Угол найдем из ΔВАС.
Рассмотрим ΔВАС - прямоугольный.
Высота, опущенная из вершины тупого угла на большее основание, делит его на части, меньшая из которых равна полуразности оснований.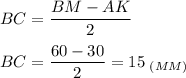
Тангенс угла - отношение противолежащего катета к прилежащему.По таблице найдем угол:
∠В ≈ 53°
2. Найдем площадь трапеции:
Площадь трапеции равна произведению полусуммы оснований на высоту.