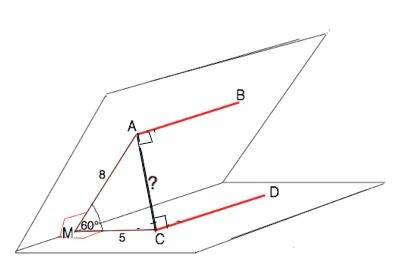
Данные отрезки параллельны линии пересечения плоскостей, следовательно, параллельны друг другу. АВ║CD.
Расстоянием между параллельными прямыми является длина отрезка, проведенного перпендикулярно к обеим прямым.
Плоскость линейного угла по определению перпендикулярна ребру двугранного угла, значит, перпендикулярна и прямым, которые параллельны этому ребру. ⇒ отрезок АС, перпендикулярный АВ и CD, - искомое расстояние между АВ и CD.
Построим линейный угол МАС двугранного угла между данными плоскостями. В треугольнике АМС угол АМС равен 60°, и по т.косинусов:
квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
АС²=8²+5*-2•8•5•cos60°
АС²=89-80•1/2
АС²=49
АС=√49=7 см - это ответ.
2(-sin(90+45))² + 6*sin(180-30) - 0 = (tg0=0)
2*sin²45 + 6sin30=2*(√2/2)² + 6*(1/2)=
2*(2/4) + 3=4.