
Это верно для произвольного 4 угольника (трапеция частный случай):
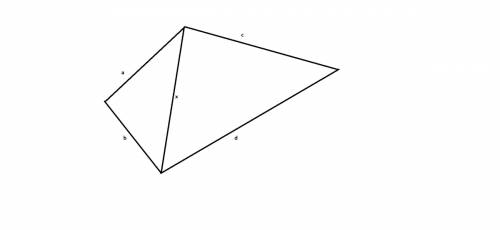
Проведем диагональ x.
Запишем неравенство треугольника abx: a+b>x ;
Запишем неравенство треугольника cdx : c+x>d ;
Сложим эти неравенства почленно: a+b+c+x>x+d .
Откуда: a+b+c>d .
Таким образом , любая сторона четырехугольника меньше суммы трех других его сторон , что ,соответственно, справедливо и для трапеции.
Ну наверное самые любознательные спросят :,,А верно ли это для произвольного многоугольника?'' Таки да это так :) . Но вот как это доказать? Пусть эта задача останется вам.Дам небольшую подсказку : примените похожий метод как для 4 угольника ,используя метод математической индукции. Удачи!
Около правильного многоугольника можно описать единственную окружность.
Доказательство:
А₁А₂А₃... - правильный многоугольник.
Пусть биссектрисы углов А₁ и А₂ пересекаются в точке О.
Так как углы А₁ и А₂ многоугольника равны, то равны и углы 1 и 2.
Тогда ΔА₁ОА₂ - равнобедренный, т.е. точка О равноудалена от вершин А₁ и А₂.
∠3 = ∠2, так как ОА₂ биссектриса, центральные углы правильного многоугольника равны (∠А₁ОА₂ = ∠А₂ОА₃), сторона ОА₂ общая для треугольников А₁ОА₂ и А₂ОА₃, значит треугольники равны по стороне и двум прилежащим к ней углам.
Тогда ОА₃ = ОА₁.
Аналогично можно доказать, что равны и остальные треугольники. Таким образом, точка О равноудалена от всех вершин, значит она - центр описанной окружности.
Эта окружность будет описана и около треугольника, например, А₁А₂А₃, а вокруг треугольника можно описать единственную окружность, значит данная окружность - единственная, которую можно описать около правильного многоугольника.
Дано: правильная пирамида, у которой сторона основания а = 14, боковое ребро L = 25.
Sбок = (1/2)РА, где Р - периметр основания, А - апофема (высота боковой грани для правильной пирамиды).
Находим апофему:
А = √(L² - (a/2)²) = √(25² - 7²) = √(625 - 49) = √576 = 24.
ответ: Sбок = (1/2)*(6*14)*24 = 1008 кв.ед.