такого треугольника не существует
или 60 см^2.
Объяснение:
Треугольника с заданными сторонами не существует.
13 см > 10см + 13мм, не выполнено неравенство для сторон треугольника.
Если в условии опечатка, длины стороны треугольника 13 см, 13 см, 10 см, то площадь может быть найдена по формуле Герона:
S = √p•(p-a)•(p-b)•(p-c).
p = (10+13+13):2 = 18 (см),
S = √18•(18-13)•(18-13)•(18-10) = √(18•5^2•8) = √(9•5^2•16) = 3•5•4 = 60 (см^2)
Ещё одним может быть нахождение по формуле
S = 1/2•a•h, где а = 10 см, а длина высоты найдена по теореме Пифагора из прямоугольного треугольника, образованного боковой стороной, высотой, проведённой к основанию, и половиной основания, h = 12 см.
(S = 1/2•10•12 = 60 (см^2) ).
Объяснение:
Дано:
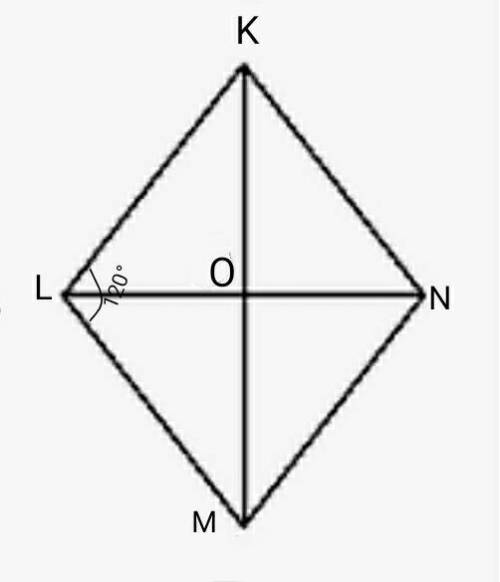
KLMN- ромб.
LN=6см
KM=10,4см.
<L=120°
<NOM=?
<OMN=?
<ONM=?
P=?
Решение.
<KLM=<KNM, свойство ромба.
Сумма углов прилежащих к одной стороне ромба равна 180°
<KLM+<LMN=180°
<LMN=180°-<KLM=180°-120°=60°
Диагонали ромба являются биссектриссами углов.
КМ- биссектрисса угла <LMN и <LKN
<OMN=<LMN:2=60°:2=30°
LN- биссектрисса угла <KNM и <KLM
<ONM=<KNM:2=120°:2=60°
Диагонали ромба пересекаются перпендикулярно.
<NOM=90°.
Рассмотрим треугольник ∆LNM
<NLM=<LNM=<LMN=60°.
Значит ∆LNM- равносторонний.
LN=NM=ML=6см.
В ромбе все стороны равны.
Р=4*LN=4*6=24см.
ответ: <NOM=90°; <ONM=60°; <OMN=30°. Периметр равен 24см.
Решение
Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам.
ОN=LN:2=6:2=3см.
ОМ=КМ:2=10,4:2=5,2см.
По теореме Пифагора найдем
MN=√(ON²+OM²)=√(3²+5,2²)=√(9+27,04)=
=√36,04≈6 см. (Округлили до сотых)
Р=4*MN=4*6=24 см.
ответ: периметр 24.
(14,4-2,7•2):2=(14,4-5,4):2=9:2=4,5 м
Объяснение: