конус
l (ВМ) = 6 см (образующая)
∠ВМО = 30°
Найти:S осн - ?
Решение:Осевое сечение конуса (секущая проходит через ось конуса) - равнобедренный треугольник, а высота Н (МО) разделяет этот треугольник на два прямоугольных треугольника.
sin(1/2 * 30˚) = R/l
sin(15˚) = R/6
sin(45˚ - 30˚) = R/6
sin(45˚) cos(30˚) - cos(45˚) sin(30˚) = R/6
(√2/3) * (√3/2) - (√2/2) * 1/2 = R/6
(√6/4) - (√2/4) = R/6
((√6) - (√2)) * 6 = 4R
(6√6) - (6√2) = 4R
4R= 6√6 - 6√2
R = (3√6) - (3√2)/2
Итак, ВО (R) = (3√6) - (3√2)/2
S осн = пR²
S осн = п((3√6) - (3√2)/2)² = 18 - 9√3п см²
ответ: 18 - 9√3п см²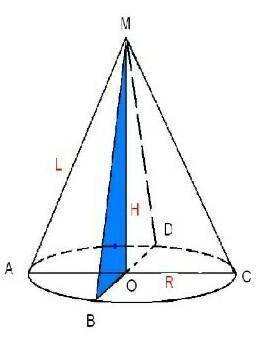
По-быстрому я в таблице набросал. Смотрите вложение Так и есть.
Смотрите 2ю картинку. Площадь заштрихованной фигуры и надо найти.
Такое чудо считается при интеграла. Т.е. площадь фигуры ограниченной графиком функции y(x) осью абцисс и в общем случае прямыми x=a и x=b (криволинейной трапеции) равна:
Где пределы интегрирования a,b нам надо определить. В нашем случае это x-координаты точек пересечения графика с осью абцисс, т. е. корни уравнения:
Решаем его (квадратное уравнение)
D=1+4*1*6=25
x₁=-2; x₂=3
Далее, подставляем в формулу площади (1) нашу функцию и пределы интегрирования
Смотрите вложение. (не хочет он, гад, принимать формулы!)
Так, площадь получилась отрицательной. Ну и правильно у нас фигура под осью x лежит. Такая штука может получиться и при вычислении мощности переменного тока на части периода. Там знак важен.
А поскольку нам надо площадь, можно записать модуль результата