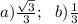
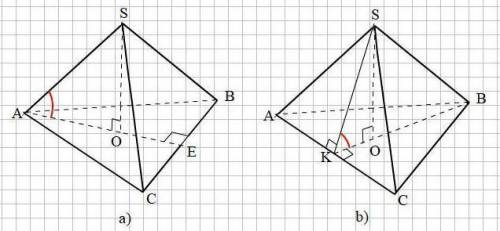
Объяснение:
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
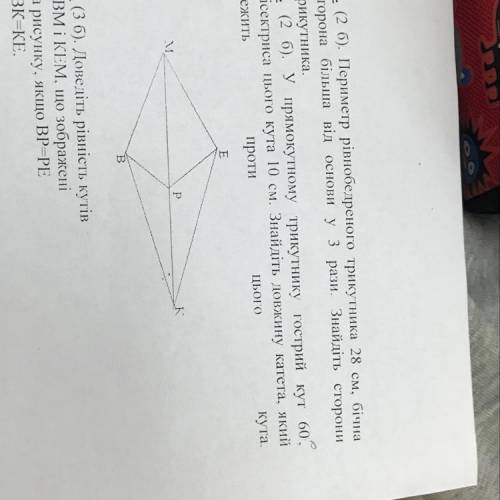
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
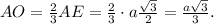
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
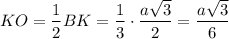
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.
Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.
Объяснение:
Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=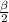
.
ΔАОК- прямоугольный ,
cos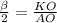
, KO=R*cos;
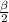sin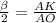
,AK=R*sin 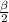,AB=α2Rsin .
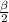ΔSKO прямоугольный ,cos α=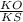
, KS=R*cos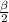/cosα.
S=0,5*AB*SK ,S=0,5*2R*sin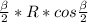
/ cosα,
S=0,5*R²*sinβ/cosα=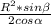
Пусть меньший катет равен х.
Биссектриса делит угол 60 градусов на 2 по 30 градусов.
Тогда отрезок большего катета между вершиной прямого угла и основанием биссектрису равен x*tg30° = x/√3.
По Пифагору (x/√3)² + x² = 10².
(x²/3) + x² = 100,
x² + 3x² = 300,
4x² = 300,
x² = 75,
x = √75 = 5√3.
ответ: больший катет равен (5√3)*tg60° = 5√3*√3 = 15 см.