
такого треугольника не существует
или 60 см^2.
Объяснение:
Треугольника с заданными сторонами не существует.
13 см > 10см + 13мм, не выполнено неравенство для сторон треугольника.
Если в условии опечатка, длины стороны треугольника 13 см, 13 см, 10 см, то площадь может быть найдена по формуле Герона:
S = √p•(p-a)•(p-b)•(p-c).
p = (10+13+13):2 = 18 (см),
S = √18•(18-13)•(18-13)•(18-10) = √(18•5^2•8) = √(9•5^2•16) = 3•5•4 = 60 (см^2)
Ещё одним может быть нахождение по формуле
S = 1/2•a•h, где а = 10 см, а длина высоты найдена по теореме Пифагора из прямоугольного треугольника, образованного боковой стороной, высотой, проведённой к основанию, и половиной основания, h = 12 см.
(S = 1/2•10•12 = 60 (см^2) ).
ответ: 30°
Объяснение:
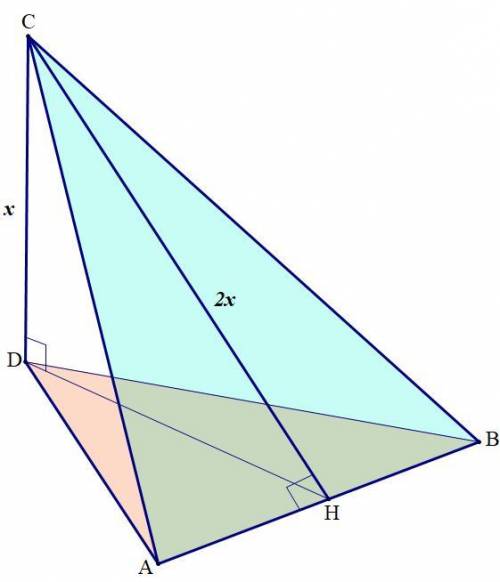
1. Расстояние от точки до прямой -- это перпендикуляр из этой точки к прямой.
CH ⊥ AB
Расстояние от точки до плоскости -- это перпендикуляр из этой точки к плоскости.
CD ⊥ (ABD)
2. CD ⊥ (ABD), DH c (ABD) ⇒ CD ⊥ DH (прямая, перпендикулярная плоскости, перпендикулярна любой прямой в этой плоскости)
3. CH -- наклонная, CD ⊥ (ABD) ⇒ DH -- проекция CH на плоскость (ABD).
4. CH -- накл., DH -- проекц., CH ⊥ AB ⇒ DH ⊥ AB (теорема о трёх перпендикулярах)
5. Угол между плоскостями -- это угол между перпендикулярами, проведёнными к их общему ребру.
(ABC) ∩ (ABD) = AB -- ребро
CH ⊥ AB, CH c (ABC); DH ⊥ AB, DH c (ABD) ⇒ ∠((ABC), (ABD)) = ∠DHC -- искомый
6. Пусть CD = x, тогда CH = 2x. Рассмотрим прямоугольный ΔCDH.
Катет в два раза меньше гипотенузы ⇒ ∠CHD = 30° (теорема об угле 30° в п/у Δ)
да являється.❤️❤️❤️❤️❤️❤️