На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH=  , FH=4√2 см=0,04√2 м
, FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)
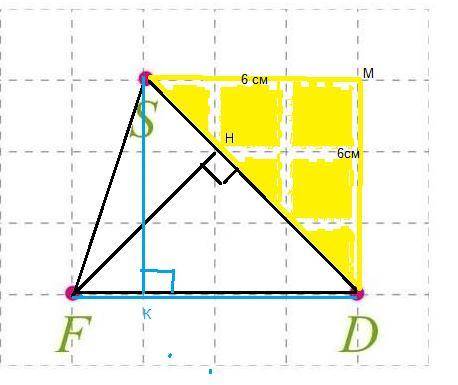
На листочке в клеточку отмечено три точки F, S, D. Известно , что площадь одной клеточки 4 см². Рассчитайте расстояние от F до SD в метрах.
Объяснение:
Расстояние это перпендикуляр. Пусть FH⊥SD. Тогда FH расстояние до SD.
Найдем длину квадрата площадью 4 см² ⇒2*2=4, значит сторона квадрата 2 см.
Пусть SК⊥FD . Найдем площадь ΔFSD
S=1/2*FD*SK , S=1/2*8*6=24 (см²).
С другой стороны S( ΔFSD)=1/2*SD*FH .Нахождение SD внизу.
24=1/2*6√2*FH ⇒FH=  , FH=4√2 см=0,04√2 м
, FH=4√2 см=0,04√2 м
Расстояние от F до SD 0,04√2 м
==================
В желтом прямоугольном треугольнике , со стороной 6 см, по т. Пифагора, SD=√(6²+6²)=√(2*6²)=6√2 ( cм)

40°, 40°, 100°
Объяснение:
Диагонали прямоугольника равны и точкой пересечения делятся пополам:
KO = MO = NO = PO
ΔKOM - равнобедренный с основанием КМ, значит углы при основании равны:
∠ОКМ = ∠ОМК
MON - внешний для треугольника КОМ и значит равен сумме двух внутренних, не смежных с ним. Тогда
∠ОКМ = ∠ОМК = ∠MON / 2 = 80° / 2 = 40°
∠КОМ = 180° - ∠MON = 180° - 80° = 100° как смежный с углом MON.