они действительно равны
Объяснение:
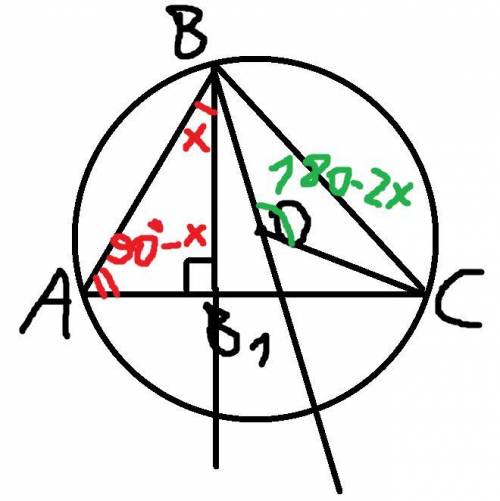
Пусть <ABB1 = x, тогда если <BB1A = 90 градусов (т.к. BB1 - высота), то ABB1 = (180 - 90 - x) градусов = (90 - x) градусов. Т.к. <BAC - вписанный для дуги BC, а <BOC - центральный для этой же дуги BC, то <BOC = 2*<BAC = 2*(90 - x)градусов = (180 - 2x) градусов. Очевидно, что BO = OC = R, тогда треугольник BOC - равнобедренный, тогда <CBO = <BCO = (180 - < BOC) / 2 = (180 - (180 - 2x)) / 2 = 2x / 2 = x. Следовательно <ABB1 = <CBO = x.
√22,25
Объяснение:
B(-2;5) Xв=-2; Ув=5
С(5;3) Хс=5; Ус=3
М(Хм;Ум)
Хм=(Хв+Ус)/2=(-2+5)/2=1,5
Ум=(Ув+Ус)/2=(5+3)/2=8/2=4
М(1,5;4)
А(4;0) Ха=4; Уа=0
АМ=√((Хм-Ха)²+(Ум-Уа)²)=√((1,5-4)²+(4-0)²)=
=√((-2,5)²+4²)=√(6,25+16)=√22,25