ответ: 80.
Объяснение:
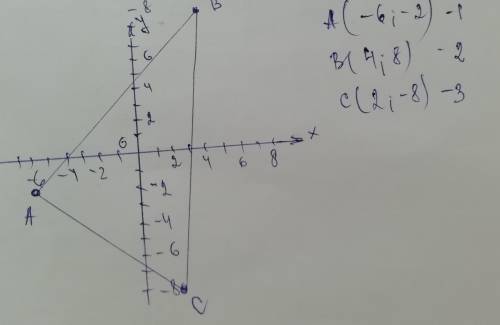
Построим координатную плоскость и нанесем точки А,В,С. (смотри чертёж).
Чтобы найти площадь при таких данных, воспользуемся формулой Герона:
S = √p(p-a)(p-b)(p-c), где a, b и c - стороны треугольника р=(a+b+c)/2 - полупериметр треугольника.
Но есть более простая формула:
S=1/2|(x2-x1)(y3-y1)-(x3-x1)(y2-y1|); (| | - по модулю);
Обозначим точки 1 - А; 2 - В; 3 - С.
Тогда S= 1/2| (4-(-6))(-8-2)-(2-(-6))(8-(-2))|=1/2| (10*(-6))-(10*10)|=1/2| (-60-100) |= 1/2 |-160|=1/2* 160=80.
1. Расстояние от центра окружности до точки, из которой проведены две касательные, делит угол A пополам. Значит угол HAO равен 30 градусам. Проведем радиус от точки O в точку касания окружности с касательной. Радиус, проведенный из центра окружности к точке касания является перпендикуляром к касательной. Получается прямоугольный треугольник HAO. В прямоугольном треугольнике катет, лежащий против угла в 30 градусов половине гипотенузы. OA - гипотенуза
OH=1/2*6
OH=3
OH-радиус окружности
ответ:R=3
2.28 градусов
3.7