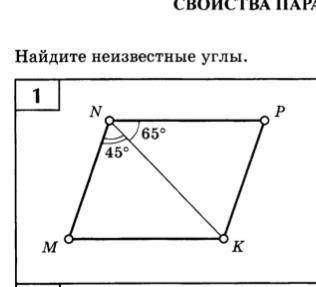
Луч NK проходит между сторонами угла МNР, поэтому ∠МNP состоит из суммы 45°+65°=110°, противолежащие углы параллелограмма равны, поэтому ∠К=∠N=110°.
Углы, прилежащие к одной стороне, в сумме составляют 180°⇒
∠М=180°-∠N= 180°-110°=70°, и опять таки противоположные углы равны, поэтому ∠Р=∠М= 70°.
ответ
∠М=70°
∠Р= 70°
∠К=110°.
Нарисуем этот треугольник.
Обозначим точки буквами- см.рисунок.
Получились прямоугольные треугольники, высоты в который определяются по формуле высоты равностороннего треугольника
h=(а√3):2
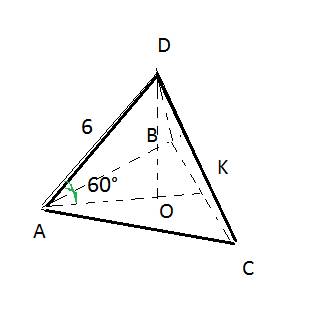
Найдем сторону ВК в треугольнике КВМ
3=(ВК√3):2
(ВК√3)=3*2=6
ВК=6:√3=2√3
По той же формуле найдем АВ
5=(АВ√3):2
АВ√3=5*2=10
АВ=10:√3=(10√3):3
АК=(10√3):3 -2√3=(10√3 -6√3):3=(4√3):3
КН=√3(4√3):3):2=12:6=2см
рисунок - во вложении
----------------------------------------------
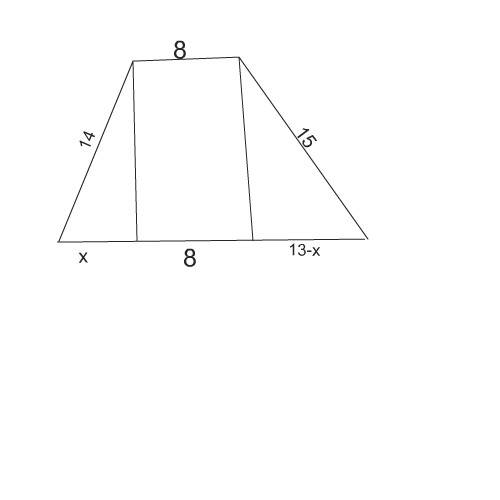
Рисуем трапецию.
Опустим из ее углов при меньшем основании высоты на нижнее основание.
Получили один прямоугольник и два прямоугольных треугольника при боковых сторонах как гипотенузах.
Найдем значение высот и приравняем их.
Для этого отрезок основания при боковой стороне 14 обозначим х, а отреок ( катет) при боковой стороне 15 будет 21-х-8=13-х
14²-х²=15²-(13-х)²
Из этого уравнения найти х, затем из прямоугоьного треугольника с гипотенузой 14 и катетом, равным найденному х, вычислить высоту трапеции.
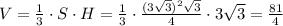 куб. см
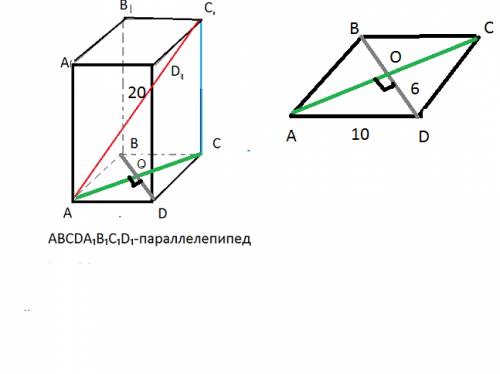
куб. см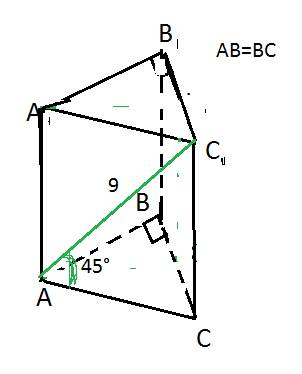
угол N= углу К = 45+65=110⁰
угол М= углк Р = 180-110=70⁰