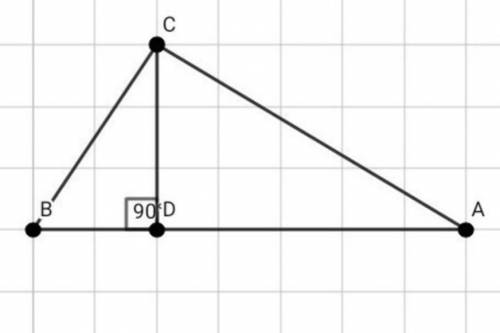
1) Рассмотрим ∆ АВС ( угол С = 90° ):
По теореме Пифагора:
АВ² = ВС² + АС²
АВ² = 8² + 6² = 64 + 36 = 100
Значит, АВ = 10 см
2) Площадь прямоугольного треугольника рассчитывается по формуле через катеты:
S = 1/2 × a × b = 1/2 × BC × AC = 1/2 × 6 × 8 = 24 см²
Но с другой стороны площадь треугольника вычисляется по стороне и высоте, проведенной к этой стороне →
S = 1/2 × AB × CD
24 = 1/2 × 10 × CD
24 = 5 × CD
Значит, CD = 24/5 = 4,8 см
ОТВЕТ: 4,8 см
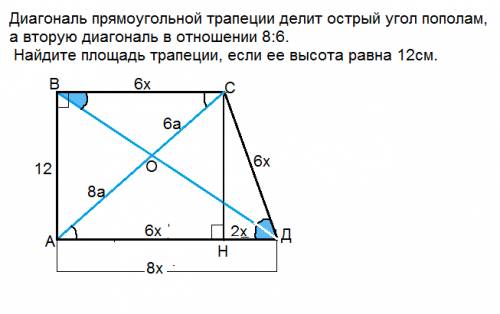
Диагональ делит угол пополам - эта диагональ - биссектриса.
Биссектриса трапеции отсекает от нее равнобедренный треугольник. В самом деле:
В треугольнике ВСД угол СВД=углу ВДА как накрестлежащие, угол ВДС=углу ВДА как половины угла АДС. Следовательно, угол ВДС=углу СВД.
ВС=СД.
В трапеции треугольники, образованные диагоналями и основаниями, - подобны. Они имеют по равному вертикальному углу при пересечении биссектрис и равные накрестлежащие углы.
k=AО:ОС=8:6
АД:ВС=8:6
Пусть коэффициент этого отношения равен х
Тогда АД=8х, ВС=6х
Опустим из С высоту СН=12.
АН=ВС, НД=8х-6х=2х, СД=ВС=6х
По т.Пифагора
СД²-НД²=СН²
36х²-4х²=144
32х²=144
х=√4,5=1,5√2 ⇒
ВС=9√2
АД=12√2
S (АВСД)=(21√2)*12:2=126√2 см²
1. См. рис.1. Найти отрезок КР. КР = МН – МК – РН.
Т.к. МН – средняя линия трапеции, то МК и РН – средние линии треугольников АВС и ДВС. У этих треугольников общее основание ВС. Следовательно МК = РН = ВС/2 = 8/2 = 4 см. Т.к. МН – средняя линия трапеции , то МН = (АД+ВС)/2 = (16 + 8)/2 = 12 см. Таким образом, КР = 12 -4 -4 = 4 см.
2. См. рис.2. Синие линии нужны для объяснения принципа построения. При построении требуемой прямой их, естественно, не будет.
Внутри угла А поставлена точка М. Через эту точку проведена прямая, пересекающая лучи «а» и «е» в точках С и В соответственно. Если эта линия будет проведена правильно, то в получившемся треугольнике АСВ МА будет медианой, поскольку должно выполниться условие СМ = МВ. Медиана делит площадь треугольника пополам. Т.е. площадь треугольника АВМ должна равняться площади треугольника АМС. Значит, площадь треугольника АВС должна равняться двум площадям треугольника АВМ. Эти треугольники (АВС и АВМ) имеют общее основание АВ. Отсюда следует, что высота РС треугольника АВС должна быть в два раза больше высоты МК треугольника АВМ. Вот это обстоятельство и необходимо использовать при построении. Теперь забыли про синие линии. Их нет.
Из точки М опустим перпендикуляр (МК) на любой из лучей угла, например, на луч «е». Затем проведем прямую параллельно лучу «е» на расстоянии СР = 2МК. Пересечение этой прямой с лучом «а» даст точку С. Проведя прямую через точки М и С построим требуемую линию.
3. См. рис. 3. Требуемое условие будет выполняться, если НК будет параллельна АС. Опять же синяя линия для объяснения принципа. Если НК параллельна АС то треугольники АВД и НВЕ подобны. Так же подобны и треугольники СДВ и КЕВ. Для первой пары подобных треугольников ВД/АД = ВЕ/НЕ. Для второй пары ВД/СД = ВЕ/ЕК. Из этих двух соотношений вытекает, что АД/ДС = НЕ/ЕК. А поскольку АД = ДС, то и НЕ = ЕК. Таким образом, что бы выполнилось требуемое условие НК должен быть параллелен АС.

CD=6,т.к. 12-6=6
AD=6, она равна CD, т.к. два угла по 45°
АС=
по теоремп Пифагора
AB=6