a)
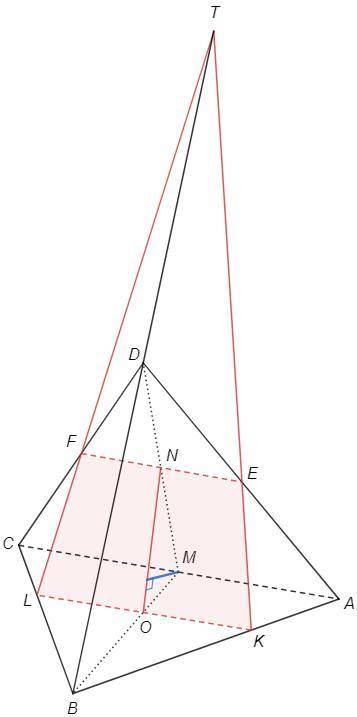
Плоскость (OEF) проходит через через среднюю линию △ADC.
EF||AC, следовательно плоскость (OEF) параллельна AC и ее след KL в грани ABC также параллелен AC, KL||AC.
По теореме о пропорциональных отрезках KL делит BC, BM, BA в равном отношении 2:1 (O - пересечение медиан, BO:OM =2:1)
Теорема Менелая для △BAD
BK/KA *AE/ED *DT/TB =1 => 2/1 *1/1 *DT/TB =1 => DT=DB
Аналогично для △BCD.
Прямые KE и LF - значит и плоскость (ОEF) - пересекают прямую DB в точке T так, что DT=DB.
б)
Плоскость (OEF) параллельна AC, достаточно найти расстояние от любой точки прямой до плоскости.
BM, DM - медианы и высоты => AC⊥(BMD) => (BMD)⊥(OEF)
ON - линия пересечения перпендикулярных плоскостей.
MH⊥ON => MH⊥(OEF), искомое расстояние.
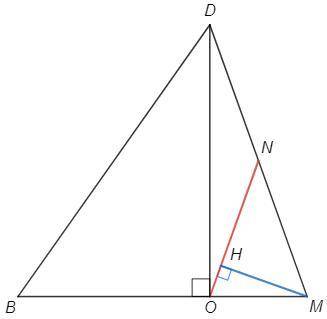
Далее решаем в плоскости (BMD)
Правильный тетраэдр, O - центр основания.
DO =√6/3 *3√6 =6 (высота правильного тетраэдра)
N - середина DM (т Фалеса)
ON=NM (медиана из прямого угла)
△ONM - равнобедренный => ∠MOH=∠DMO
△MOH~△DMO => MH/DO =OM/DM
BM=DM, BO/OM =2/1 => OM/DM =1/3 => MH =DO/3 =2
Sastd = 67,5+15√3 см².
Объяснение:
Площадь боковой поверхности пирамиды ASTD - это сумма площадей боковых граней ATS, ADS и ATD, так как по принятому обозначению пирамиды ее вершина обозначается первой.
Площадь грани ADS (правильного треугольника) равна
Sads = √3*а²/4 = √3*100/4 = 25√3 см².
Площадь грани ATD (прямоугольного треугольника) равна
Satd = (1|2)*AT*AD = 30 см².
Площадь грани ATS равна
Sasb = Sads = 25√3 см², так как площади граней равны.
Площади треугольников АST и BST имеют общую высоту (высоту грани ASB) и относятся как стороны, к которым проведена эта высота, то есть Sats/Sbts = 3/2. А так как Sasb = Sats+Sbts, то
Sats/Sasb = 3/5. тогда
Sats = (3/5)*Sasb = (3/5)*25√3 = 15,5 см².
Площадь боковой поверхности пирамиды ASTD равна:
Sastd = 25√3 + 30 + 37,5 = 67,5+15√3 см².
P.S. На всякий случай:
Площадь грани STD можем найти по Герону.
По теореме косинусов в треугольнике AST:
ST² = √(AT²+AS²-2*AT*AS*Cos60). (угол SAT = 60, так как грани - правильные треугольники). Тогда
ST = √(136-2*AT*AS*(1/2)) = √76.
DT = √(AT²+AD²) = √136.
SD = 10.
Полупериметр равен (10+√136+√76)/2 и по Герону:
Sstd = √((10+√136+√76)*(10+√76-√136)*(10+√136-√76)*(√136+√76-10))/4 или
Sstd = √((10+√76)²-136)*(136-(10-√76)²)/4 или
Sstd = √((20√76+40)*(20√76-40))/4 или
Sstd = √((30400-1600)/4 = √28800/4 = 120√2/4 =30√2.