Відповідь:
p 20
Пояснення:
В условии ошибка: ВС ║AD, а не АС, так как параллельные прямые не могут проходить через одну точку.
BF = DE по условию,
∠AED = ∠CFB по условию,
∠CBF = ∠ADE как накрест лежащие при пересечении параллельных прямых ВС и AD секущей BD, ⇒
ΔCBF = ΔADE по стороне и двум прилежащим к ней углам.
Значит CF = AE,
BE = BF - EF, DF = DE - EF, а так как BF = DE, то и BE = DF,
∠CFD = ∠AEB как смежные с равными углами (∠AED = ∠CFB по условию),
значит ΔCFD = ΔAEB по двум сторонам и углу между ними.
Тогда ∠АВЕ = ∠CDF, а эти углы - накрест лежащие при пересечении прямых АВ и CD секущей BD, значит АВ║CD.

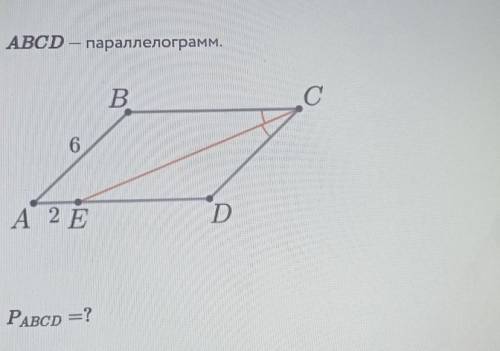
28ед
Объяснение:
АВ=CD, свойство параллелограма.
<ВСЕ=<СЕD, внутренние накрест лежащие.
<СЕD=<ECD. → ∆ECD- равнобедренный (углы при основании равны).
ЕD=DC=6ед
АD=AE+ED=2+6=8 ед.
Р(ABCD)=2(AB+AD)=2(6+8)=2*14=28ед