

Расстояние от моста до пристани катер преодолел на 2 часа быстрее, чем расстояние от пристани до моста. Найдите собственную скорость катера, если скорость течения 2 км/ч, а расстояние между пристанью и мостом 48 км.
Объяснение:
Пусть собственная скорость катера х км/ч , х>0,
тогда скорость катера против течения (х-2) км/ч. ,
а скорость по течению (х+2) км/ч .
Время катера против течения 48/(х-2) ч,
а время катера по течению 48/(х+2) км/ч.
Т.к время катера против течения на 2 часа больше , то составим уравнение : 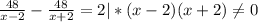 ,
,
48(х+2)-48(х-2)=2(х-2)(х+2) ,
49х+96-48х+96=2х²-8,
2х²=192+8,
х²=100 ⇒ х=10.
ответ. Собственная скорость катера 10 км/ч.
ВК=2, АК=8, тогда, АВ=10.
Центр вписанной окружности лежит в точке пересечения биссектрис треугольника, проведём биссектрису ВН: точка Н совпадёт с точкой касания окружности на стороне АС, т.к. в биссектриса, проведённая из угла В, является и высотой, и медианой, т.е. угол АНС = 90 градусов.
АН=АК, т.к. отрезки касательных, проведённых из одной точки, равны, т.е. АН=8, тогда АС=16.
В прямоугольном треугольнике АВН АВ=10, АН=8, тогда по теореме Пифагора ВН=6.
Найдём площадь треугольника: 1/2 * АС * ВН = 1/2 * 16 * 6 = 42.