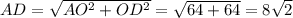
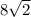
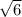и ВС=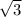
. АС - гипотенуза, АС=3. Чтобы узнать проекции катетов на гипотенузу, надо из вершины прямого угла опустить перпендикуляр на гипотенузу. Пусть это будет ВМ. Тогда АМ - проекция АВ, МС - проекция ВС. Пусть АМ=х, тогда МС=3-х, потому что АС=3. Тогда по формуле среднего геометрического ВМ=
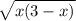. А теперь рассмотрим прямоугольный треугольник АВМ. Запишем теорему Пифагора: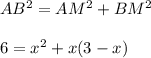
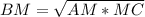
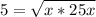
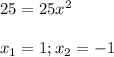
Длина такого отрезка равна высоте, опущенной на основание, деленной на КОСИНУС угла отрезка с этой высотой.
Косинус - монотонно убывающая функция (между 0 и 180, между 0 и 90 она еще и положительна, а у нас именно такой случай), что легко видно из координатного определения (асбцисса радиуса единичной окружности, чем больше угол, тем меньше координата конца радиуса - в интервале углов от 0 до 90).
Поэтому длина отрезка будет монотонно возрастать. Пока конец отрезка не достигнет вершины (конца основания).
Есть еще какая-то теорема, что в треугольнике против большего угла лежит большая сторона, применение этой теоремы к треугольнику, образованному отрезком, боковой стороной и куском основания, сразу решает задачу... но я не помню, как эта теорема доказывается без применения тригонометрии: