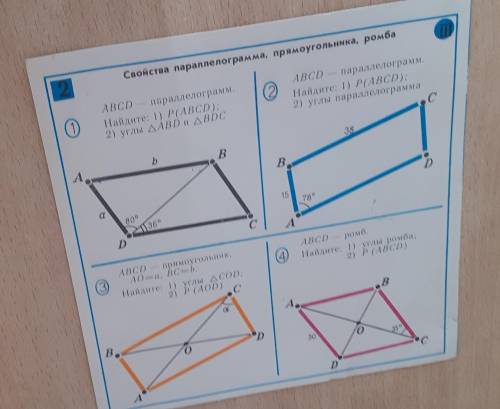
2114 кв.см
Объяснение:
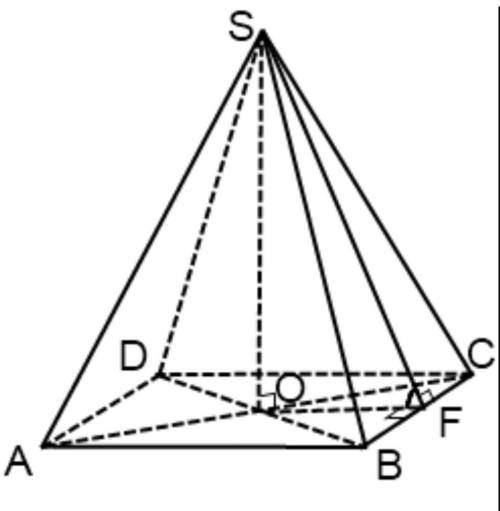
Пирамида в Лувре представляет собой правильную четырёхугольную пирамиду (прототип пирамиды Хеопса)
Правильная четырехугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — квадрат, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр пересечения диагоналей квадрата основания из вершины.В основании пирамиды находится квадрат площадью 1225 кв.м. Значит сторона квадрата равна:
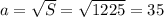
Высота пирамиды- SO=21,6
Для нахождения полной площади поверхности пирамиды нужно сложить площадь боковой поверхности и площадь основания.Sполн. = Sбок. + Sосн.
Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему:Sбок=p×l
р=Р/2=4а/2=2а=2×35=70 см
Апофему SF найдём из прямоугольного треугольника SFO(<O=90°) по теореме Пифагора.
SO=21,6 - по условию. ОF= 1/2×AB=1/2×35=17,5 см
Sбок=70×12,7=889 кв.см
Sполн= 889+1225=2114 кв.см
Відповідь:
Пояснення:
1) Р=2×(а+b)
<D=<B=36+80=116°
<A=<C=180-116=64°
2)P=2×(15+38)=106
<A=<C=78°
<Br<D=180-78=102°
3) Так как диагонали в прямоугольнике равни, то CO=OD и угли при основе CD равни, то угоди СОD=180-2×aльфа
Р(AOD)=1/4×P(ABCD)=1/2×(a+b)
4) P(ABCD)=4×30=120
<C=<A=2×35=70° так как АС есть и биссектриса
<B=<D=180-70=110°