Две прямые, перпендикулярные одной и той же плоскости, параллельны.
PP1 ⊥ ,
QQ1 ⊥ => PP1 II QQ1
Через 2 параллельные прямые можно провести плоскость и притом только одну .
PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Две точки А и А' плоскости называются симметричными относительно прямой с, если эта прямая проходит через середину отрезка АА' и перпендикулярна к нему. Каждая точка прямой c считается симметричной самой себе.
Соответствие, при котором каждой точке А сопоставляется симметричная ей относительно прямой с точка А', называется осевой симметрией. Прямая с называется осью симметрии.
Две фигуры F и F' называются симметричными относительно оси с, если каждой точке одной фигуры соответствует симметричная точка другой фигуры.
Фигура F называется симметричной относительно оси с, если она симметрична сама себе.
Примем без доказательства, что при симметрии прямые переходят в прямые, причем сохраняются расстояния и углы.
Представление об осевой симметрии дает перегибание листа бумаги. При этом линия сгиба будет осью симметрии, а каждая точка листа совместится с симметричной точкой.
В природе оси симметрии имеют листья деревьев, лепестки цветов, бабочки, стрекозы и мн. др
PP1Q1Q-квадрат
Периметр равен 41,2 см
Объяснение:
Две прямые, перпендикулярные одной и той же плоскости, параллельны.PP1 ⊥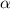 ,
,
QQ1 ⊥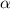 => PP1 II QQ1
=> PP1 II QQ1
Через 2 параллельные прямые можно провести плоскость и притом только одну .PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.=>PQ II P1Q1
PQQ1P1 - параллелограмм.
Так как < PP1Q1, <QQ1P1 равны 90°, то
PQQ1P1 - прямоугольник.
PP1=PQ => PQQ1P1 - квадрат.
Периметр квадрата находится по формуле:
Р=4а=4×10,3= 41,2 см