ответ: 18° ( возможно Вы ошиблись записывая ответы? и в ответе Е 18 °)
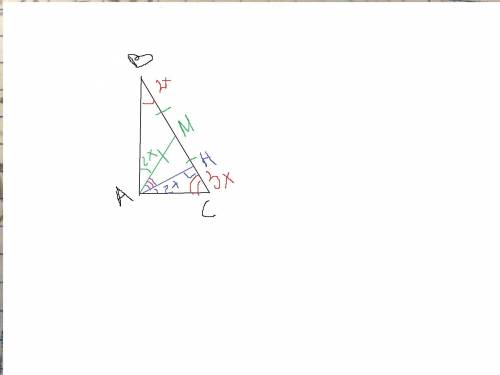
Дано: ΔАВС, ∠А=90°,∠А:∠В=2:3, АМ- медиана, АН- высота
Найти: ∠МАН-?
Пусть ∠В=2х, ∠С=3х, тогда по теореме о сумме острых углов треугольника:
2х+3х=90°;
5х=90°;
х=90°:5;
х=18°.
∠В=2*18°=36°
∠С=3*18°=54°.
Рассмотрим ΔАНС, где ∠Н=90°, ∠С=54°, следовательно
∠НАС=90°-54°=36°.
Так как АМ- медиана, то вокруг треугольника АВС можно описать окружность с центром в точке М и по свойству медианы, проведённой из прямого угла к гипотенузе она равна половине гипотенузы. То есть АМ=ВМ=СМ.
Рассмотрим ΔАВМ, так как АМ=ВМ, то треугольник равнобедренный, следовательно ∠В=∠АВМ=36° как углы при основании равнобедренного треугольника.
∠МАН=∠А-∠АВМ-НАС=90°-36°-36°=18°
Вариант 1: АС = √13 см.
Вариант 2: АС = 5 см.
Объяснение:
В треугольнике АВС АВ=3√2, ВС=1, АС=√2*R (дано). Найти АС.
По теореме синусов: АС/sinB = 2R. => R√2/SinB = 2R.
SinB = √2/2. Значит угол равен 45 градусов и cosB=√2/2. По теореме косинусов:
АС²= АВ²+ВС² - 2АВ*ВС*cosB. Подставляем значения и получаем
АС² =18+1 - 2*3√2*1*√2/2 =13.
АС = √13 см.
Второй вариант:
Угол при вершине В тупой и тогда косинус этого угла отрицательный и равен -√2/2. Тогда
АС²= АВ²+ВС² + 2АВ*ВС*cosB = 18+1 + 6 =25.
АC = √25 = 5 см.
Проверка по теореме о неравенстве треугольника:
Вариант 1: АВ≈4,24; ВС=1; АС≈3,6. 4,24 < 3,6+1. Треугольник существует.
Вариант 2: АВ≈4,24; ВС=1; АС=5. 5 < 4,24+1. Треугольник существует.
Відповідь:
Пояснення:
Есть 2 варианта
1 ОС и ОД сонаправление
ОСД
ОС=3/5ОД
СД=30
СД=ОД-ОС=ОД-3/5ОД=2/5 ОД
ОД=30×5÷2=75
ОС=75-30=45