Решение в объяснении
Объяснение:
На бумаге проводим прямую, на ней отмечаем точку A - вершина будущего угла. От данного угла, из его вершины строим произвольную окружность, окружность с таким же радиусом строим и от точки A, пересечение с прямой обозначим B. Теперь от окружности у данного угла отмеряем расстояние между точками пересечений. С таким радиусом строим окружность в точке B, Точку Пересечения окружностей с центрами в точке А и в точке В соединяем отрезком с точкой А. Данный угол будет искомым
Ну либо просто чертим с транспортира
Объяснение:
1.Угол, вершина которого лежит в центре окружности называется
А) центральным;
2. Угол, вершина которого лежит на окружности называется
Б) вписанным;
3. Вписанный угол равен
В) половине дуги на которую он опирается.
4. Центральный угол равен
Б) дуге, на которую он опирается;
5. Чему равен вписанный угол, опирающийся на дугу в 120°
Б) 60°;
6. Чему равен центральный угол, опирающийся на дугу в 40°
В) 40°
7. Чему равен вписанный угол, опирающийся на дугу в 100°
А) 50°;
8.Чему равен центральный угол, опирающийся на дугу в 80°
Б) 80°;
Запишите ответ (задания 9-12):
9. Найдите <DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
<DEF опирaтeся на дугу = 360°-(DE + EF)=360°-( 150° + 68° ) =142°.
<DEF - вписанный угол,
<DEF=1/2×142°=71°
10. Найдите <KOM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°. Точка O — центр окружности.
υMK=υKN-υMN=180°-124°=56°
<KOM - центральный угол,<KOM=56°
11. Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.
<C - вписанный угол,= половине центральнoго углa AOB.
<C=1/2<AOB=1/2*48°=24°
12. Точка О — центр окружности, <AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах). Дай рисунок.
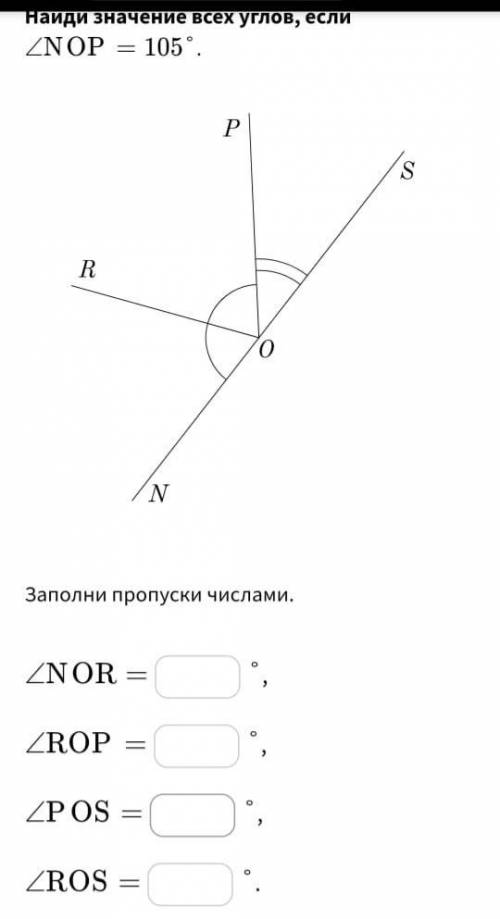
1)Учитывая то обстоятельство, что все углы смежные при прямой NOS, а значит:
{< - угол}; <NOR+<ROS=180°;
а так же <NOP+<POS=180°;
Поэтому зная значение <NOR или <ROP, можно найти истинное значение<POS,
2)Поскольку OR является биссектрисой <NOP, делящей угол пополам, то
3)Из пункта 1 следует, что <POS=180°-105°=75°
4) Последний угол можно найти суммой двух других, а именно:
<ROS=<ROP+<POS, значения которых уже известны.
<ROS=52,5°+75°=127,5°
ответ: 52,5°; 52,5°; 75°; 127,5°.