
Ни один из вариантов не подходит.
Объяснение:
Задача: Катеты прямоугольного треугольника равны 2 см и 4 см, Найдите катеты подобного ему прямоугольного треугольника, гипотенуза которого равна 6 см.
Итак, по теореме Пифагора гипотенуза данного нам треугольника равна с = √(4²+2²) = √20 = 2√5 см.
Коэффициент подобия треугольников - отношение сходственных сторон (гипотенуз) равен k = 6/2√5.
Cледовательно, k² = 36/20 = 1,8.
Зная, что отношение площадей подобных фигур равно квадрату коэффициента подобия, а площадь данного нам прямоугольного треугольника равна половине произведения его катетов, то есть 4 см², попробуем отыскать из данных вариантов нужные нам катеты прямоугольного треугольника, площадь которого равна S = k²·4 = 1,8·4 = 7,2 cм².
При всем желании сочетания катетов из предложенных нам вариантов, при котором
S = (1/2)·a·b = 7,2 см² нет:
А) S = (1/2)·3,2·4,4 = 7,04 см².
В) S = (1/2)·3,4·4,6 = 7,82 см².
С) S = (1/2)·3,6·4,8 = 8,64 см².
D) S = (1/2)·3,3·4,2 = 6,93 см².
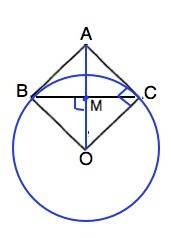
Отрезки касательных из одной точки до точки касания с окружностью равны. По свойству радиуса, проведенного в точку касания, ОВ⊥ВА; ОС⊥СА
∆ АВО=∆ АСО по 3-м сторонам ( по каким - укажите)
∆ ВАС - равнобедренный, ∠ ВАМ=∠САМ,
АМ биссектриса, высота, медиана ∆ ВАС и перпендикулярна ВС.
АМ=МО по условию, следовательно, ВМ - медиана прямоугольного треугольника, проведенная к гипотенузе, и
ВМ=АМ=ОМ (свойство), ⇒ ВС=АО
Четырехугольник, диагонали которого равны, взаимно перпендикулярны и при пересечении делятся пополам - квадрат.
⇒
∠ВАС=90°
1)г
2)д
3)а
4)Б
Якщо буде таке ж саме завдання то ви малюєте координатну пряму і визначаєте точки 1 координата завжди на прямій Х друга на У і визначаєте (1,2,3,4 )в яких вона знаходиться