Геометрия: Дан треугольник acb. ac=5 ac1=3. найти чему равна медиана cc1

Дан треугольник acb. ac=5 ac1=3. найти чему равна медиана cc1

👇

Увидеть ответ

Ответ:

AlinaLay

28.11.2020

ответ показан на фотографии, я там доказал их равенство, это не нужно, зарешался)

Дан треугольник acb. ac=5 ac1=3. найти чему равна медиана cc1

4,8(88 оценок)

Открыть все ответы

Ответ:

13SCHOOL13

28.11.2020

1)Пусть х см - a

(3х)см-b

S=ab

3x^2=27

x1=-3 -не удовлетворяет,так как <0

x2=3

а=3 см

b=9 см

ответ:3 см;9 см

2)Sквадрата=а^2

а^2=64 см

а=8 см

Р=а*4

Р=8*4=32 см

ответ:32 см

3)У ромба все стороны равны,а сторон 4.

Р=4*а

а=16:4

а=4 см

S=а*h(высота)

16=4*h

h=4 см

ответ:4 см

4)S=1/2 *AB(гипотенуза)*h(высота)

1/2*АВ*4=40

АВ=20 см

ответ:20 см

5)Так как трапеция прямоугл.,то большая сторона и является высотой

S=(ВС+AD)/2 *h(высота)

S=(5+13)/2*10

S=90 см^2

ответ:90 см^2

6)Сумма углов многоугольника равна 180*(n-2),где n-количество сторон

у нас сумма углов 180*3=540 градусов

Пусть х градусов приходится на одну часть

15х=36

х=36 градусов

36 градусов-первый угол

72 градусов-2 угол

108 градусов-3 угол

144 градуса-4 угол

180 градуса-5 угол

8)пусть 1 катет-х см, 2 катет-(х+2)

По теореме Пифагора находим х

х^2+x^2+4x+4=100

x^2+2x-48=0

D=49

x1=-8 - <0 не удовлетворяет

х2=6

1 катет-6 см

2 катет-8 см

Площадь прямоугольного треугольника равна половине произведения катетов.

S=6*8/2=24 кв.см.

ответ:24 кв.см.

4,4(8 оценок)

Ответ:

Kurgan4511

28.11.2020

Площадь боковой поверхности цилиндра равна периметру основания, умноженного на высоту, то есть S = 2*pi*R*H. R = AO = OB, H = OO1. S = 2*pi*R*OO1. Рассмотрим нижнее основание - окружность с центром О: дуга АВ равна бета, центральный угол равен радианной или градусной мере дуги, на которую опирается, а поскольку дуга АВ = бета, следовательно, центральный угол АОВ = бета. С этих пор обозначим угол альфа - α, бета - β. Из равнобедренного треугольника АОВ (поскольку АО = ВО - радиусы) <OAB = <OBA = (180-β)/2 = 90 - β/2. По теореме синусов: AB/sin(β) = R/sin(90-β/2), из таблицы формул приведения аргумента имеем: sin(pi/2-р) = cos(р), поскольку pi/2 = 90 градусов, а угол р = β/2, имеем: AB/sin(β) = R/cos(β/2), AB = (R*sin(β))/cos(β/2). Найдем теперь высоту OK: OK^2 = OB^2 - (BK)^2, OK^2 = OB^2 - (AB/2)^2, OK^2 = R^2 - ((R*sin(β))/2cos(β/2))^2. Рассмотрим треугольник ABO1: AO1 = BO1, следовательно треугольник ABO1 равнобедренный, а следовательно, <O1AB = < O1BA = (180 - α)/2 = 90 - α/2. Аналогично предыдущему, по теореме синусов: AB/sin(α) = AO1/sin(90-α/2), sin(90-α/2) = cos(α/2). Имеем: AO1 = (AB*cos(α/2))/sin(α) = (R*sin(β)*cos(α/2))/sin(α)*cos(β/2).
Рассмотрим прямоугольный треугольник я это лучше распишу на картинке. И площадь боковой поверхности тоже.

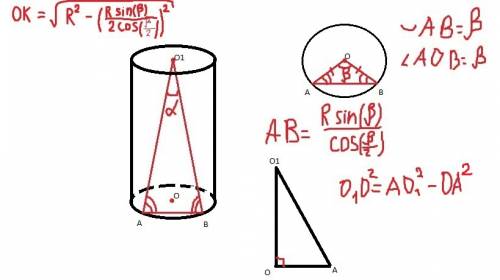
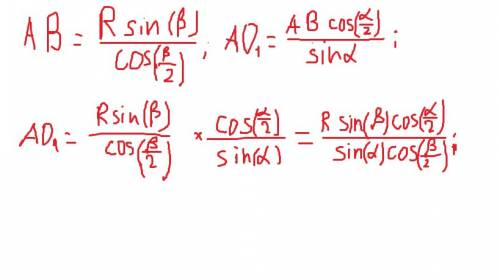
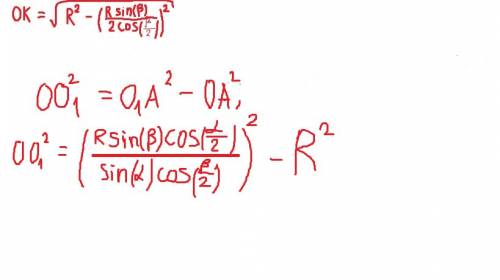
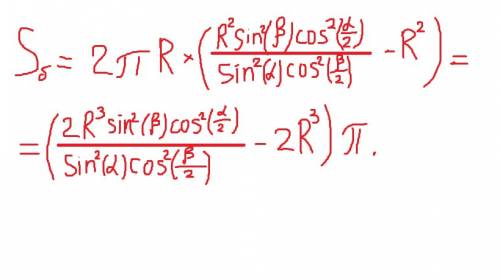
Вцилиндре параллельно его оси, проведена плоскость, которая пересекает нижнее основание по хорде, ко