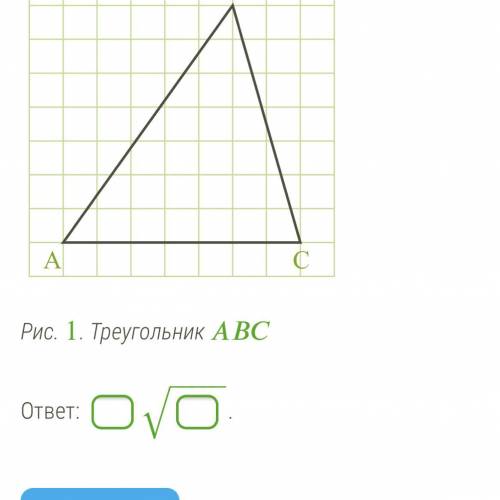
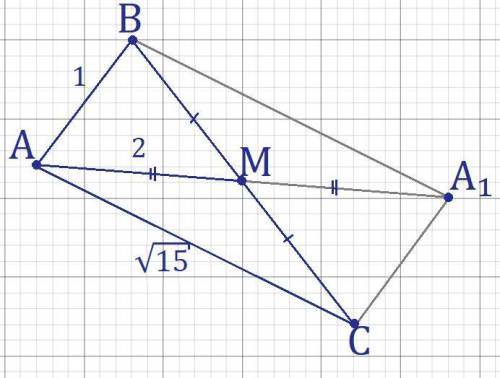
Дано: AB=1; AC=√15; BM=MC; AM=2.
Найти: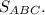 
A₁ ∈ AM; AM=A₁M
ABA₁C - параллелограмм т.к. диагонали делятся точкой пересечения пополам (BM=MC по условию; AM=MA₁ по построению), поэтому A₁C=AB=1.
ΔAA₁C - прямоугольный т.к. выполняется теорема Пифагора:
AA₁² = (2AM)² = (2·2)² = 4² = 16;
AC²+CA₁² = (√15)²+1² = 15+1 = 16;
16 = 16 ⇒ AA₁² = AC²+CA₁².
Поэтому ∠ACA₁ = 90°, он лежит на против гипотенузы AA₁.
ABA₁C - прямоугольник т.к. это параллелограмма с углом в 90° (∠ACA₁=90°), поэтому ∠BAC=90°.
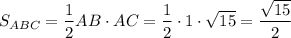как площадь прямоугольного треугольника (∠BAC=90°).
ответ: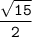 
ABCD-Ромб
Bd=13см(меньшая диагональ)
BH=12см
Найти S
у Треугольника BDH угол H=90 градусов,BD=13,BH=12cm теперь по тиареме Пифагора:
HD=Под Корнем BD(D в квадрате)-BH(Hв квадрате)=под корнем 13в квадрате-12в квадрате=5 см
теперь 2 у трегуольника ABH Угол h=90 градусов,BH=12,AH=AD-HD=(AB-5)cm теперь по теореме пифагора
AB(B в квадрате)=AH(H в квадрате)+BH(H в квадрате)
AB(B в квадрате)=(AB-5)в квадрате+12 в квадрате
AB(B в квадрате)=AB(B в квадрате)-10AB+25+144,10AB=169
AB=16.9
и Теперь Находим площадь
S=Ab умножить на BH=16,9 умножить на 12=202,8см(см в квадрате)
S=202.8см