Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
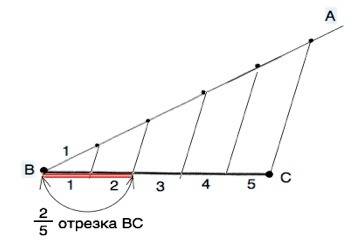
Пусть дан отрезок ВС.
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
60 градусов каждый угол треугольника АВД
Объяснение:
1)Треугольник АВД равнобедренный, т.к. стороны АД=АВ. Значит высота, проведенная из вершины А к основанию ВД, является еще и медианой и биссектрисой. В этом случае ВС=СД.
2)Рассмотрим один из получившихся прямоугольных треугольников, например, АВС. В треугольнике мы видим, что ГИПОТЕНУЗА В ДВА РАЗА БОЛЬШЕ КАТЕТА, А ЭТО ЗНАЧИТ,ЧТО УГОЛ,НАПРОТИВ ЭТОГО КАТЕТА РАВЕН 30 ГРАДУСОВ.(ВАС)
3)Так как треугольник прямоугольный найдём его третий угол АВС 180-30-90=60 ГРАДУСОВ.
4)Далее, вспоминаем, что АВД- РАВНОБЕДРЕННЫЙ треугольник и вспоминаем, что углы при его основании равны, значит, АВД=АДВ=60 ГРАДУСОВ.
5)И теперь находим угол ДАВ 180-60-60=60 ГРАДУСОВ. Треугольник равносторонний, все углы по 60 градусов.
ИЛИ
2)Т.к. ВС=СД, ТО ВД=ВС=СД=7
3)Так как все стороны 7, то треугольник равносторонний, и все его углы равны. (180/3=60 градусов)
25°
Объяснение:
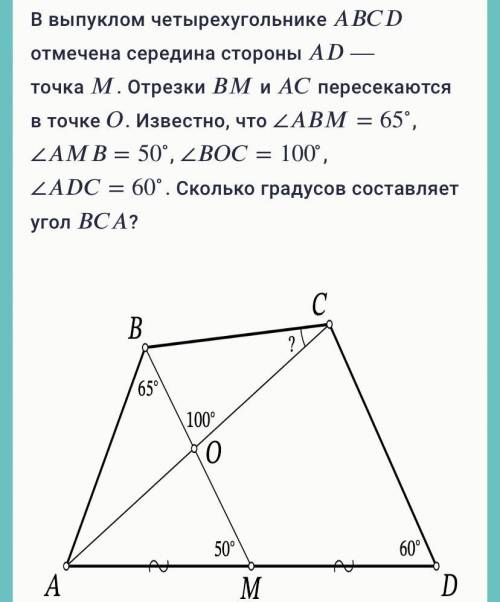
Дано: ABCD - выпуклый четырехугольник.
∠АВМ=65°; ∠АМВ=50°; ∠ВОС=100°; ∠АDC=60°.
Найти: ∠ВСА.
1. Рассмотрим ΔАВМ.
Сумма углов треугольника равна 180°.
⇒ ∠А=180°-(∠АВМ+∠АМВ)=180°-(65°+50°)=65°
⇒ ΔАВМ - равнобедренный (углы при основании равны)
АМ=МВ.
2. Рассмотрим ΔАОМ.
Вертикальные углы равны.
⇒∠ВОС=∠1=100°
∠2=180°-(∠1+∠ОМВ)=180°-(100°+50°)=30°
3. Рассмотрим ΔАСD
∠АСD=180°-(∠2+∠D)=180°-(30°-60°)=90°
⇒ ΔАСD прямоугольный.
СМ - медиана (АМ=МD)
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
⇒ АМ=МС=MD
4. Рассмотрим ΔАСМ.
АМ=МС (п.3) ⇒ ΔАСМ - равнобедренный.
⇒ ∠2=∠3=30° (углы при основании р/б треугольника равны)
∠АМС=180°-(∠2+∠3)=180°-60°=120°
5. Рассмотрим ΔВМС.
АМ=МВ (п.1)
АМ=МС (п.3)
⇒МВ=МС ⇒ΔВМС - равнобедренный.
∠5=∠ВСМ (углы при основании р/б треугольника равны)
∠4=∠АМС-∠АМВ=120°-50°=70°
⇒ ∠5=∠ВСМ=(180°-∠4):2=(180°-70°):2=55°
6. ∠ВСА=∠ВСМ-∠3=55°-30°=25°