32 ед².
Объяснение:
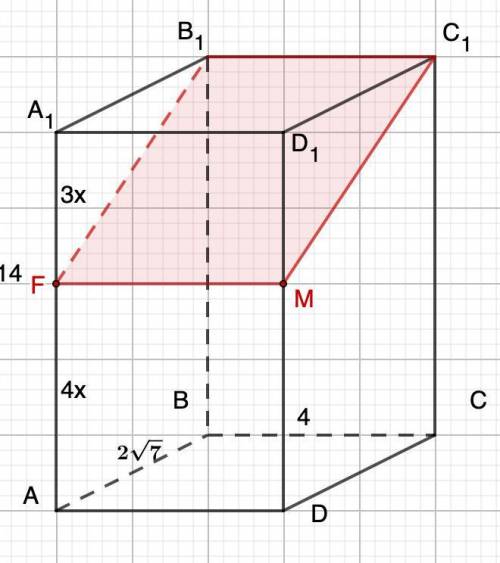
Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед.
F∈AA₁, A₁F:FA = 3:4
BC = 4; AB = 2√7; AA₁=14.
Через точки F, B₁,C₁ проходит сечение.
Найти: площадь сечения.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.Противоположные грани параллелепипеда параллельны.⇒ сечение FB₁C₁C - прямоугольник.
Площадь прямоугольника равна произведению смежный сторон.⇒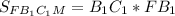 
1. Пусть А₁F = 3x, тогда AF = 4x, а АА₁ = 7х = 14
7х = 14 ⇒ х = 2
Тогда A₁F = 3x = 6
2. Рассмотрим ΔFA₁B₁ - прямоугольный.
A₁F = 6; A₁B₁ = AB = 2√7;
По теореме Пифагора найдем FB₁:
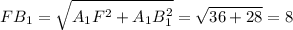
Теперь найдем площадь сечения:
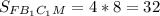(ед.²)
Но известно, что AD=22, значит ОD=16.
ДАЛЕЕ по теорему Пифагора рассчитаем сторону треугольника СЕ. Так как СЕ - гипотенуза то она равна 12 ( 16*16+20*20=корень из 144=12.
Теперь нам известна высота, и мы можем найти площадь трапеции.
Площадь трапеции= сумма оснований разделить на два и умножить на высоту= (6+22/2)*12=168 см в квадрате.