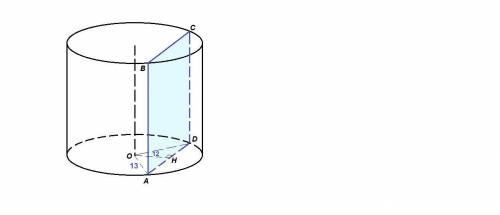
Радиус основания цилиндра равен 13 см, площадь сечения цилиндра плоскостью, параллельной оси цилиндра, равна 80 см², расстояние от плоскости сечения до оси цилиндра равно 12 см. Найдите высоту цилиндра
.
ответ: 8 см
Объяснение:
OA = OD = R = 13 см
Проведем ОН⊥AD. ОН лежит в плоскости основания, АВ - перпендикуляр к плоскости основания, значит ОН⊥АВ.
Тогда ОН⊥(АВС),
ОН = 12 см - расстояние от оси цилиндра до плоскости сечения.
ΔАОН: ∠АНО = 90°, по теореме Пифагора
АН = √(АО² - ОН²) = √(13² - 12²) = √(169 - 144) = √25 = 5 см
ОН - высота равнобедренного треугольника AOD, значит ОН и медиана, ⇒
AD = 2АН = 10 см
ABCD - прямоугольник,
Sabcd = AD · АB = 80
АB = Sabcd : AD = 80 : 10 = 8 см
Ширина реки равна длине расстояния СН, измеренного перпендикулярно между ее берегами, иначе - высоте СН треугольника АВС. .
Алгоритм решения:
а) По т.синусов вычислим АС,
б) вычислим площадь ∆ АВС.
в) из площади найдем высоту СН, равную ширине реки.
—————
а ) Угол С=180°- (угол А+угол В)
угол А=12°30’=12,5°
B=72°42’=72,8°
Угол С=180°-(12,5°+72,8°=94,8°
АВ:sin 72,8=AC:sn 94,8°
sin 72,8=0.95476
sin94,8°=0.99649 , откуда АВ=67.0684
б) S (ABC)=AC•AB•sin(CAB):2
S (ABC)=508
CH=2S:AC=1016:70=14,5 м