(см. объяснение)
Объяснение:
Приведу 2 решения. Алгебраическое и логическое. Выбирай то, которое тебе проще.
Алгебраический метод:
Достоинства: универсален. Можно решить любую задачу этого рода.
Недостатки: присутствуют вычисления. Есть возможность ошибиться в расчетах. Длительность решения, вызванная расчетами.
Подставляй вместо x число, в каждое уравнение и считай y. Смотри, на каком графике есть полученная координата.
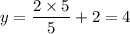
Точка (5; 4) есть только на графике А.
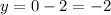
Точка (0; -2) есть только на графике Б.
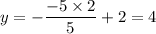
Точка (-5; 4) есть только на графике В.
Тогда получили ответ: А-1, Б-2, В-3.
Решение, основанное на логических рассуждениях:
Достоинства: нет расчетов. Шанс ошибиться стремится к 0. Скорость решения. Используя этот метод можно моментально решать подобные задачи.
Недостатки: требуется соответствующее мышление. Хорошее понимание темы. Знание того, за что отвечает каждый коэффициент в уравнении каждого графика функции.
Рассмотрим графики А, Б и В. Заметим, что график В принципиально отличается от графиков А и Б наклоном прямой. За наклон отвечает число перед x. В вариантах ответа 1 и 2 такие числа одинаковые: 2/5. Значит сразу понятно соответствие B-3. Рассмотрим графики А и Б. Они отличаются тем, что один из них выше другого. За это отвечает число b, (если y=kx+b). Т.е. мы смотрим на число без буквы x. Там, где оно со знаком +, это график А, где со знаком -, то это график Б.
АС1/С1В=1/1, ВА1/А1С=3/7, АВ1/В1С=1/3, S A1B1C1=S ABC - S AC1B1 - S C1BA1 - S A1CB1, обе части уравнения делим на S ABC
S A1B1C1 / S ABC = 1 - (S AC1B1/S ABC) - (S C1BA1/ S ABC) - (S A1CB1/S ABC)
S ABC=1/2*AB*AC*sinA, S AB1C1=1/2*AC1*AB1*sinA, AB=AC1+C1B=1+1=2, AC=AB1+B1C=1+3=4, S AB1C1/S ABC=(AC1*AB1)/(AB*AC)=(1*1)/(2*4)=1/8,
S ABC=1/2*AB*BC*sinB, S C1BA1=1/2*C1B*BA1*sinB, BC=BA1+A1C=3+7=10,
S C1BA1/S ABC=(C1B*BA1)/(AB*BC)=(1*3)/(2*10)=3/20,
S ABC=1/2*AC*BC*sinC, S A1CB1=1/2*A1C*B1C*sinC, S A1CB/S ABC=(A1C*B1C) / (AC*BC)=(7*3)/(4*10)=21/40,
S A1B1C1/S ABC=1-1/8-3/20-21/40=8/40=1/5, или S ABC/S A1B1C1=5/1