В равнобедренном треугольнике высота к основанию является также биссектрисой и медианой.
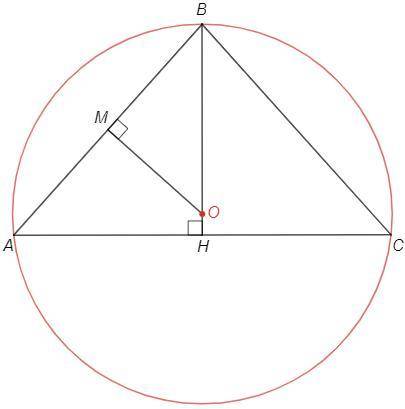
BH - высота/биссектриса/медиана
AC=4x, AB=3x
AH =AC/2 =2x
BH =√(AB^2 -AH^2) =√(9-4) x =√5 x (т Пифагора)
Центр вписанной окружности - пересечение биссектрис.
AI - биссектриса
По теореме о биссектрисе
BI/IH =AB/AH =3/2 => IH =2/5 BH =8 (см)
Центр описанной окружности - пересечение серединных перпендикуляров.
MO - серединный перпендикуляр к AB
AB/BH =3/√5 => AB =3/√5 BH =12√5
△OBM~△ABH (прямоугольные с общим углом)
OB/AB =BM/BH => OB/12√5 =6√5/20 => OB =18 (см)
Или
cosA =2/3
sinC =sinA =√(1 -cosA^2) =√5/3
AB =BH/sinA
AB/sinC =2R (т синусов) => R =BH/2sinA^2 =20/2 :(5/9) =18 (см)

А(100, -14)
3*100+13= (-14)
313=(-14)
Не належить
В(-18,41)
3*(-18)+13=41
-54+18 = 41
-41=41
Належить
Объяснение:
А(100, -14), В(-18,41)
Проверим точку А
Первая цифра, (100 в нашем случае) отвечает за х, а вторая (в нашем случае (-14)) за у.
Подставляем:
(для удобства переносим у назад, чтобы вышло понятное уравнение)
3*100+13= (-14)
313=(-14) - 313 не = (-14), поэтому, точка "А" не принадлежит графику.
Проверим точку В
Первая цифра, ((-18) в нашем случае) отвечает за х, а вторая (в нашем случае 41) за у.
Подставляем:
3*(-18)+13=41
-54+18 = 41
-41=41 - точка "В" принадлежит, так как противоположная
130°
Объяснение:
Пусть ВМ = х, тогда АВ = 2х.
Продлим медиану ВМ за точку М на ее длину, ВМ = МК = х
ВК = 2х.
Тогда АВСК - параллелограмм (диагонали точкой пересечения делятся пополам),
СК = АВ = 2х, тогда
ΔВСК равнобедренный с основанием ВС. Углы при основании равны:
∠КСВ = ∠КВС = 50°, ⇒
∠ВКС = 180° - (∠КСВ + ∠КВС) = ∠180° - 100° = 80°
∠КВА = ∠ВКС = 80° как накрест лежащие при АВ║СК (противоположные стороны параллелограмма) и секущей ВК.
∠АВС = ∠СВМ + ∠КВА = 50° + 80° = 130°