Объяснение:
Все высоты находим по теореме Пифагора
Первый треугольник:
Высота к стороне Б равна: √(17²-8²)=√225=15
Высота к боковой стороне равна: (2√(p(p-a)(p-b)²)/b=(2√(25х9х64))/17=(2х5х3х8)/17=240/17=14.12см
p - полупериметр, равен (17+17+16)/2=25
а - основание
б - боковая сторона
ответ: 15 и 14.12см
Вторая задача:
По формуле h=(2√(p(p-a)(p-b)(p-c)))/a
p - полупериметр, равен 40
ha=(2√(40x10x6x24))30=480/30=16
hb=(2√(40x10x6x24))34=480/34=240/17=14.12
hc=(2√(40x10x6x24))16=480/16=30
ответ, 16, 30 и 14.12см
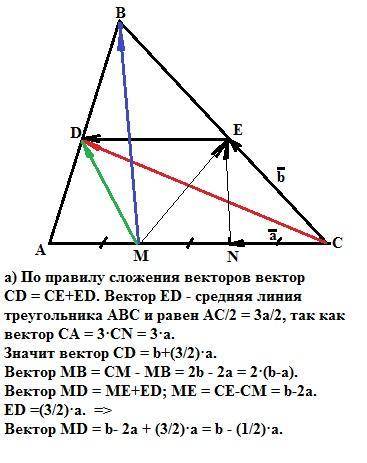
а) CD= b+(3/2)·a. MB= 2·(b-a). MD= b- (1/2)·a.
б) доказательство в объяснении.
Объяснение:
a) По правилу сложения векторов вектор CD = CE+ED. Вектор ED - средняя линия треугольника АВС и равен АС/2 = 3а/2, так как вектор СА = 3·СN = 3·a. Значит вектор CD = b+(3/2)·a.
Вектор МВ = СМ - MB = 2b - 2a = 2·(b-a).
Вектор MD = ME+ED; ME = CE-CM = b-2a. ED =(3/2)·a. =>
Вектор MD = b- 2a + (3/2)·a = b - (1/2)·a.
б) Вектор NE = b-a. Вектор МВ = 2·(b-a). Следовательно, вектор NE СОНАПРАВЛЕН вектору МВ, то есть, параллелен ему, что и требовалось доказать.
∠AOE = 45
∠KOM = 57
∠EOM = 102